▷ Campo eléctrico uniforme

En este post se explica qué es un campo eléctrico uniforme y cuándo se produce. También encontrarás cómo calcular el valor de un campo eléctrico uniforme y, además, un ejemplo resuelto paso a paso.

Índice

¿Qué es un campo eléctrico uniforme?

Un campo eléctrico uniforme es un campo eléctrico que tiene la misma intensidad, dirección y sentido en todos los puntos, es decir, el valor de un campo eléctrico uniforme es constante.

El campo eléctrico uniforme se da cuando hay dos placas paralelas cargadas eléctricamente con signo diferente. En general, la intensidad del campo eléctrico varía según la distancia entre las cargas, no obstante, cuando tenemos dos placas metálicas infinitas con carga eléctrica, el campo eléctrico generado es uniforme.

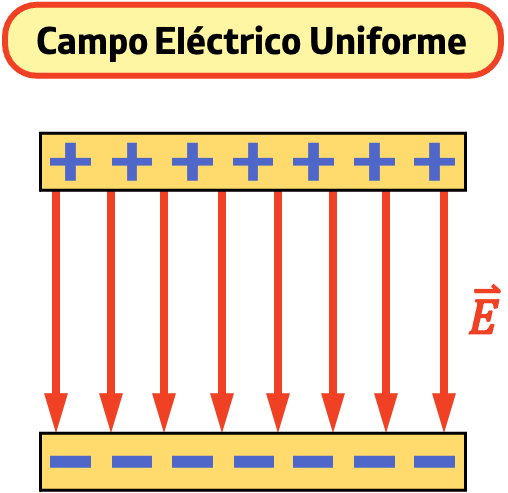
Un ejemplo real de un campo eléctrico uniforme se puede encontrar en un condensador plano paralelo cargado. Cuando se aplica una diferencia de potencial entre las placas del condensador, se crea un campo eléctrico uniforme entre ellas. Este campo eléctrico es uniforme porque la distancia entre las placas es constante y las placas son planas y paralelas.

Por otro lado, un campo eléctrico no uniforme se define como aquel que no es constante, de manera que su intensidad, dirección o sentido varía según la posición de la partícula.

➤ Ver: Líneas de campo eléctrico

Fórmula del campo eléctrico uniforme

La intensidad de un campo eléctrico uniforme entre dos placas cargadas eléctricamente es igual a la diferencia de voltaje entre las dos placas dividido por la distancia que las separa.

Por lo tanto, la fórmula del campo eléctrico uniforme es E=ΔV/d.

$E=\cfrac{\Delta V}{d}$

Donde:

$E$ es la intensidad del campo eléctrico uniforme.
$\Delta V$ es la diferencia de potencial entre las dos placas.
$d$ es la distancia que hay entre las dos placas.

Ten en cuenta que la dirección de un campo eléctrico uniforme es perpendicular a la dirección en la que se extienden las placas, además, el sentido del campo eléctrico uniforme va desde la placa con carga positiva hacia la placa con carga negativa.

Ejercicio resuelto del campo eléctrico uniforme

Tenemos dos placas metálicas paralelas separadas por 8 cm, una de las cuales está en contacto con el ánodo (+) y la otra con el cátodo (-) de una pila cuya diferencia de potencial es de 20 V. Calcula:
1. La intensidad del campo eléctrico uniforme.
2. El trabajo que hace la fuerza eléctrica cuando una carga q=5 mC se desplaza 2 cm en la dirección y sentido del campo eléctrico.

Para calcular el campo eléctrico uniforme tenemos que utilizar la fórmula que hemos visto arriba:

$\begin{aligned}E&=\cfrac{\Delta V}{d}\\[1.1ex] E&=\cfrac{20}{0,08} \\[1.1ex] E&=250 \ \cfrac{N}{C}\end{aligned}$

Ahora que sabemos la intensidad del campo eléctrico uniforme, podemos determinar el valor de la fuerza eléctrica que actúa sobre la carga:

$\begin{aligned}F&=q\cdot E\\[2ex] F&=0,005 \cdot 250 \\[2ex] F&=1,25 \ N\end{aligned}$

Finalmente, calculamos el trabajo de la fuerza eléctrica con su fórmula correspondiente:

$\begin{aligned} W&=F\cdot \Delta r \cdot \text{cos}(\alpha)\\[2ex]W&= 1,25 \cdot 0,02 \cdot \text{cos}(0º)\\[2ex]W&= 0,025 \ J\end{aligned}$

Movimiento de partículas en un campo eléctrico uniforme

En física, se suele combinar el concepto de campo eléctrico uniforme con los conocimientos de cinemática y dinámica para resolver problemas. Así pues, vamos a analizar el movimiento de una partícula cargada en un campo eléctrico uniforme.

Movimiento de partículas que inciden en la dirección del campo eléctrico uniforme

Cuando una partícula cargada eléctricamente entra en un campo eléctrico uniforme y su velocidad inicial tiene la misma dirección que el campo, actúa una fuerza eléctrica sobre ella con la misma dirección y por tanto la partícula acelera.

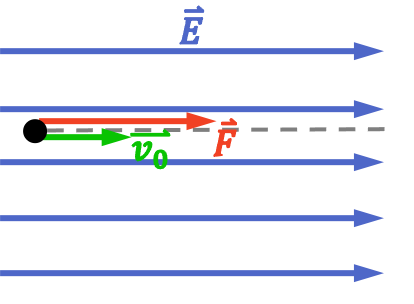
Nota: ten en cuenta que el sentido de la fuerza eléctrica depende del signo de la carga. Si la carga es negativa, el sentido de la fuerza eléctrica es opuesto al sentido del campo eléctrico.

En este caso, la partícula no se mueve en la dirección perpendicular al campo, pero en la dirección del campo tenemos un movimiento rectilíneo uniformemente acelerado (MRUA), cuya ecuación es:

$x=x_0+v_0\cdot (t-t_0) +\cfrac{1}{2}\cdot a \cdot (t-t_0)^2$

Movimiento de partículas que inciden perpendicularmente al campo eléctrico uniforme

Cuando una carga puntual entra en un campo eléctrico uniforme y su velocidad inicial es perpendicular a la dirección del campo, actúa una fuerza eléctrica sobre ella perpendicular a su dirección de movimiento.

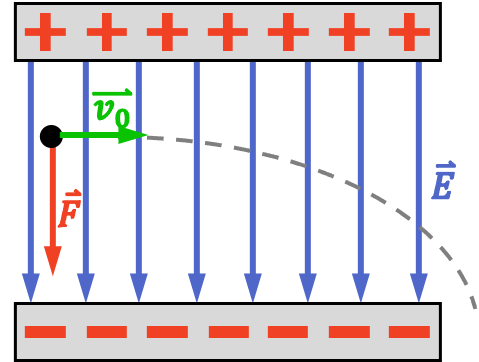
En este caso, la partícula tiene un movimiento rectilíneo uniforme (MRU) en la dirección perpendicular al campo eléctrico, mientras que describe un movimiento rectilíneo uniformemente acelerado (MRUA) en la dirección del campo eléctrico. Por tanto, sus ecuaciones de movimiento son las siguientes:

$\begin{cases}x=x_0+v_0\cdot (t-t_0)\\[2ex]y=y_0+v_0\cdot (t-t_0) +\cfrac{1}{2}\cdot a \cdot (t-t_0)^2\end{cases}$