▷ Interferencia de ondas (física)

En este post se explica qué es la interferencia de ondas en física. Así pues, encontrarás qué significa que dos ondas interfieran, los tipos de interferencia de ondas, ejemplos de interferencias de ondas y, por último, la fórmula que describe la interferencia de dos ondas.

Índice

¿Qué es la interferencia de ondas?

En física, la interferencia de ondas es un fenómeno que se produce cuando dos o más ondas se cruzan. Es decir, la interferencia de ondas consiste en la superposición de dos o más ondas para formar una onda nueva.

Así pues, la onda resultante de la interferencia de dos ondas es la suma de las ondas originales. Por lo tanto, para obtener la ecuación de dos ondas que interfieren, simplemente tenemos que sumar sus respectivas ecuaciones. Más abajo veremos cuál es la ecuación de la interferencia de dos ondas.

Por ejemplo, si lanzamos dos piedras en un estanque de agua, el impacto de cada piedra generará una onda que se propagará por el agua. Entonces, las dos ondas generadas se cruzarán y se producirá la interferencia de las dos ondas, de modo que se originará una onda resultante de la suma de las dos ondas originales.

Ten presente que la interferencia es un fenómeno físico que puede darse con todos los tipos de ondas: ondas de luz, ondas de radio, ondas de sonido, etc.

Tipos de interferencia de ondas

En física, hay dos tipos de interferencias de ondas:

Interferencia de ondas constructiva: tipo de interferencia de ondas que se produce cuando las ondas que se superponen están en fase.
Interferencia de ondas destructiva: tipo de interferencia de ondas que se produce cuando las ondas que se cruzan están en antifase.

A continuación se explica cada tipo de interferencia de ondas detalladamente.

Interferencia de ondas constructiva

La interferencia de ondas constructiva se produce cuando dos o más ondas que tienen la misma frecuencia y que están en fase se superponen. En consecuencia, la onda resultante de la interferencia constructiva de dos ondas es una onda con una amplitud mayor.

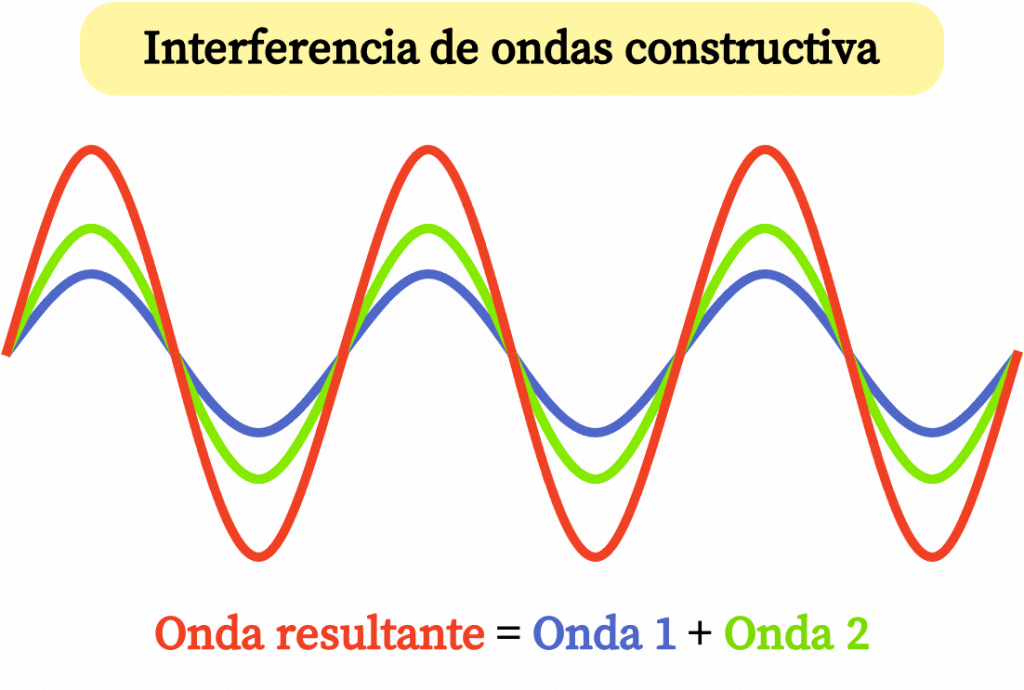
Interferencia de ondas destructiva

La interferencia de ondas destructiva se produce cuando dos o más ondas en antifase (desfasadas 180º) con la misma frecuencia se superponen. En consecuencia, la onda resultante de la interferencia destructiva es una onda con una amplitud menor, en ocasiones en una interferencia destructiva las ondas se anulan entre sí.

Ejemplos de interferencias de ondas

Una vez hemos visto la definición de la interferencia de ondas y cuáles son los diferentes tipos de interferencias de ondas, vamos a ver ejemplos de este fenómeno físico para acabar de entender el concepto.

A continuación puedes ver dos ejemplos de ondas que interfieren. En el primer ejemplo las ondas se anulan, así que se trata de una interferencia de ondas destructiva. Mientras que en el segundo ejemplo las ondas generan una onda con una amplitud mayor y, por tanto, la interferencia de las ondas es constructiva.

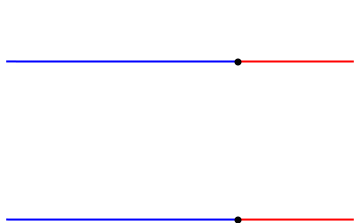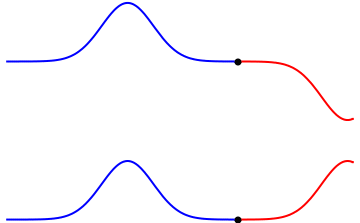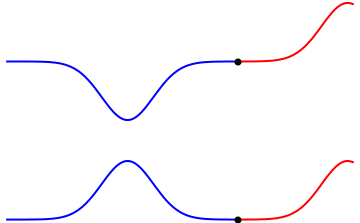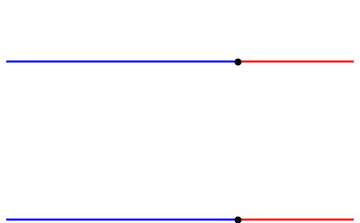
ejemplos de interferencias de ondas (física)

Fíjate que después de producirse el fenómeno de la interferencia de las ondas, las ondas iniciales mantienen su forma original y continuan propagándose en su dirección.

En física, el principio de superposición de ondas establece que la onda resultante de la interferencia entre dos o más ondas es la suma de cada una de las ondas por separado. Como puedes comprobar en la figura de arriba, cuando dos ondas se cruzan, entonces se superponen y dan lugar a una onda resultante nueva que es la suma de las ondas originales.

Por último, cabe destacar que las ondas estacionarias también son un ejemplo de la interferencia de dos ondas. De hecho, las ondas estacionarias son un tipo de ondas que se estudian en física porque tienen unas características muy peculiares debido a que se originan por la interferencia de dos ondas.

➤ Ver: ¿Qué son las ondas estacionarias?

Fórmula de la interferencia de ondas

La fórmula de la interferencia de dos ondas viene dada por la suma de las ecuaciones de las dos ondas iniciales. Así pues, la ecuación de la interferencia de dos ondas es y=2·A·sen[k·(x₁+x₂)/2-ω·t+φ/2]·cos[k·(x₁-x₂)/2-φ/2].

$\displaystyle y=2\cdot A\cdot \text{sen}\left(\frac{k(x_1+x_2)}{2}-\omega\cdot t+\frac{\phi}{2}\right)\text{cos}\left(\frac{k(x_1-x_2)}{2}-\frac{\phi}{2}\right)$

Donde:

$y$ es la elongación del punto estudiado.
$A$ es la amplitud de las ondas originales.
$k$ es el número de onda.
$x_1,x_2$ es la distancia del punto de estudio hasta el foco de la onda 1 y de la onda 2 respectivamente.
$\omega$ es la frecuencia angular o pulsación.
$t$ es el instante de tiempo.
$\phi$ es el desfase entre las dos ondas iniciales.

Ten en cuenta que si las dos ondas que interfieren se originan desde el mismo punto, se cumple que x₁=x₂=x. Por tanto, en tal caso, la ecuación de la interferencia de dos ondas queda de la siguiente manera:

$\displaystyle y=2\cdot A\cdot \text{sen}\left(k\cdot x-\omega\cdot t+\frac{\phi}{2}\right)\text{cos}\left(\frac{\phi}{2}\right)$

Recuerda que el número de onda y la frecuencia angular de una onda se calculan mediante las siguientes fórmulas:

$\begin{array}{c}k=\cfrac{2\pi}{\lambda}\\[4ex]\omega=\cfrac{2\pi}{T}=2\pi f\end{array}$

Donde:

$k$ es el número de onda.
$\lambda$ es la longitud de onda.
$\omega$ es la frecuencia angular o pulsación.
$T$ es el periodo.
$f$ es la frecuencia.

Ver demostración de la ecuación de la interferencia de dos ondas

Dadas las ecuaciones de dos ondas de propagación con la misma frecuencia y la misma amplitud pero con un desfase de un determinado ángulo φ:

$\begin{array}{c}y_1=A\cdot \text{sen}(k\cdot x_1-\omega\cdot t)\\[3ex]y_2=A\cdot \text{sen}(k\cdot x_2-\omega\cdot t+\phi )\end{array}$

La onda resultante de la interferencia de las dos ondas es la suma de las dos ondas oscilatorias, por lo tanto, la ecuación de la interferencia de dos ondas será la suma algebraica de las dos ecuaciones anteriores:

$\begin{array}{c}y=y_1+y_2\\[3ex]y=A\cdot \text{sen}(k\cdot x_1-\omega\cdot t)+A\cdot \text{sen}(k\cdot x_2-\omega\cdot t+\phi )\end{array}$

A continuación aplicaremos la siguiente fórmula trigonométrica:

$\displaystyle\text{sen}(A)+\text{sen}(B)=2\cdot \text{sen}\left(\frac{A+B}{2}\right)\cdot\text{cos}\left(\frac{A-B}{2}\right)$

Así pues, aplicando las fórmula trigonométrica anterior llegamos a la ecuación de la interferencia de dos ondas:

$\begin{array}{c}\displaystyle y=A\text{sen}(kx_1-\omega t)+A\cdot \text{sen}(kx_2-\omega t+\phi)\\[4ex]\displaystyle y=2A\text{sen}\left(\frac{(kx_1-\omega t)+(kx_2-\omega t+\phi)}{2}\right)\text{cos}\left(\frac{(kx_1-\omega t)-(kx_2-\omega t+\phi)}{2}\right)\\[4ex]\displaystyle y=2A\text{sen}\left(\frac{k(x_1+x_2)}{2}-\omega t+\frac{\phi}{2}\right)\text{cos}\left(\frac{k(x_1-x_2)}{2}-\frac{\phi}{2}\right)\end{array}$