En este artículo se explica qué es en física el movimiento circular uniformemente acelerado (MCUA), también llamado movimiento circular uniformemente variado (MCUA). También encontrarás las características del MCUA y todas las fórmulas de este tipo de movimiento circular.
Índice
¿Qué es el movimiento circular uniformemente acelerado (MCUA)?
El movimiento circular uniformemente acelerado (MCUA), también llamado movimiento circular uniformemente variado (MCUV), es un movimiento que describe un cuerpo móvil que gira alrededor de un eje con una aceleración angular constante. Por lo tanto, la velocidad angular de un MCUA varia de manera uniforme.
Por ejemplo, la rueda de un automóvil cuando arranca sigue un movimiento circular uniformemente acelerado (MCUA). Asimismo, un ventilador cuando se apaga o el giro de una peonza también son ejemplos de movimientos circulares uniformemente acelerados.
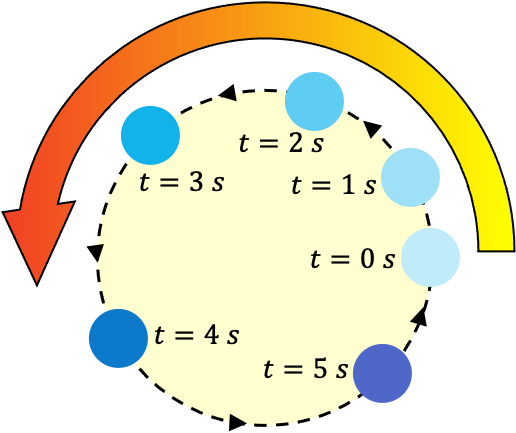
La diferencia entre un movimiento circular uniformemente acelerado (MCUA) y un movimiento circular uniforme (MCU) es el valor de la velocidad angular. En un MCU la velocidad angular es constante, en cambio, en un MCUA la velocidad angular aumenta o disminuye en el tiempo.
Características del movimiento circular uniformemente acelerado
Un movimiento circular uniformemente acelerado (MCUA) tiene las siguientes características:
- La principal característica del movimiento circular uniformemente acelerado (MCUA) es que la aceleración angular (α) es constante. En consecuencia, la velocidad angular de un MCUA no es constante, sino que aumenta o disminuye en el tiempo de manera lineal.
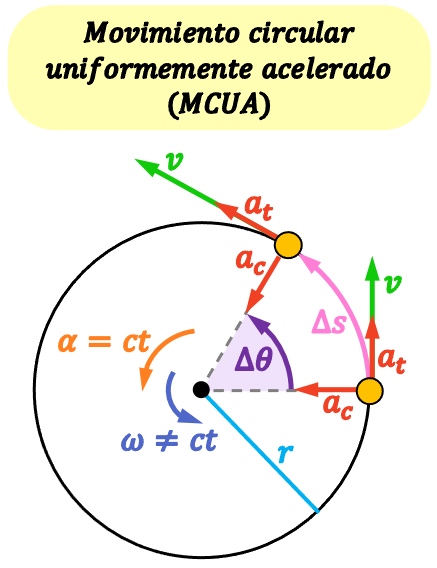
- La velocidad del cuerpo (v) que describe un movimiento circular uniformemente acelerado es tangente a la trayectoria circular, por eso se llama velocidad tangencial o velocidad lineal. La velocidad del cuerpo aumenta o disminuye en el tiempo de manera lineal.
- La aceleración centrípeta (o aceleración normal) es la componente vectorial de la aceleración del móvil que provoca el cambio de dirección de su velocidad y, por tanto, es la causa de la trayectoria circular. La aceleración centrípeta (ac) es perpendicular a la velocidad tangencial y apunta hacia el centro de la trayectoria circular.
- La aceleración tangencial (at) es tangente a la trayectoria y es la componente vectorial de la aceleración del móvil que provoca el cambio del módulo de su velocidad. Por lo tanto, si la aceleración angular es positiva, la aceleración tangencial también será positiva y la velocidad tangencial aumentará. Por otro lado, si la aceleración angular es negativa, la aceleración tangencial también será negativa y la velocidad tangencial disminuirá.
Fórmulas del movimiento circular uniformemente acelerado
A continuación, veremos cuáles son todas las fórmulas del movimiento circular uniformemente acelerado (MCUA), también conocido como movimiento circular uniformemente variado (MCUV). Estas fórmulas nos permitirán resolver ejercicios de este tipo de movimientos.
Posición angular
La posición angular se refiere al ángulo recorrido por el móvil que describe un movimiento circular uniformemente acelerado. Así pues, la fórmula para calcular la posición angular de un móvil que hace un MCUA es la siguiente:
Donde:
es la posición angular final, expresada en radianes.
es la posición angular inicial, expresada en radianes.
es la velocidad angular inicial.
es el tiempo transcurrido.
es la aceleración angular.
Velocidad angular
La velocidad angular es la velocidad a la que gira el móvil que describe el MCUA. De manera que la velocidad angular indica cuánto de rápido cambia la posición angular un cuerpo.
En un movimiento circular uniformemente acelerado (MCUA), la velocidad angular aumenta o disminuye de manera lineal en función del tiempo. Por lo tanto, en este caso la velocidad angular de un instante es igual a la velocidad angular inicial más el producto de la aceleración angular por el tiempo transcurrido.
Donde:
es la velocidad angular.
es la velocidad angular inical.
es la aceleración angular.
es el instante de tiempo en el que se calcula la velocidad angular.
Aceleración angular
La aceleración angular indica el cambio que experimenta la velocidad angular de un cuerpo. Es decir, la aceleración angular representa la velocidad a la que varia la velocidad angular.
En un movimiento circular uniformemente acelerado la aceleración angular es constante, por lo que se calcula mediante la siguiente fórmula:
Donde:
es la aceleración angular.
es la variación de la velocidad angular.
es la variación del tiempo.
es la velocidad angular final.
es la velocidad angular inicial.
es el instante de tiempo final.
es el instante de tiempo inicial.
Velocidad tangencial
La velocidad tangencial (o velocidad lineal) es la velocidad tangente a la trayectoria de un movimiento circular, es decir, la velocidad tangencial es la velocidad instantánea que tiene un cuerpo que hace un movimiento circular en un instante determinado.
La fórmula para calcular la velocidad tangencial de un cuerpo que describe un movimiento circular uniformemente variado (MCUV) es la siguiente:
Asimismo, la velocidad tangencial de un instante es equivalente a la velocidad angular de ese mismo instante multiplicado por el radio de la trayectoria:
Donde:
es la velocidad tangencial.
es la velocidad tangencial inicial.
es la aceleración tangencial.
es el tiempo transcurrido.
es la velocidad angular en el instante de tiempo en el que se calcula la velocidad tangencial.
es el radio de la trayectoria circular.
Aceleración tangencial
La aceleración tangencial (o aceleración lineal) es la aceleración tangente a la trayectoria de un movimiento circular. Es decir, la aceleración tangencial indica la variación de la velocidad tangencial de un cuerpo que hace un movimiento circular.
En un movimiento circular uniformemente acelerado (MCUA) la aceleración tangencial es constante, de modo que se puede determinar aplicando la siguiente fórmula:
Asimismo, la aceleración tangencial es equivalente a la aceleración angular multiplicado por el radio de la trayectoria:
Donde:
es la aceleración tangencial.
es la aceleración angular.
es la variación de la velocidad tangencial.
es la variación del tiempo.
es la velocidad tangencial final.
es la velocidad tangencial inicial.
es el instante de tiempo final.
es el instante de tiempo inicial.
es la aceleración angular.
es el radio de la trayectoria circular.
Aceleración centrípeta
La aceleración centrípeta (o aceleración normal) es igual al cuadrado de la velocidad tangencial partido por el radio de la trayectoria. Asimismo, la aceleración centrípeta también se puede calcular multiplicando el cuadrado de la velocidad angular por el radio de la trayectoria.
Donde:
es la aceleración centrípeta (o aceleración normal).
es la velocidad tangencial.
es el radio de la trayectoria del movimiento circular.
es la velocidad angular.
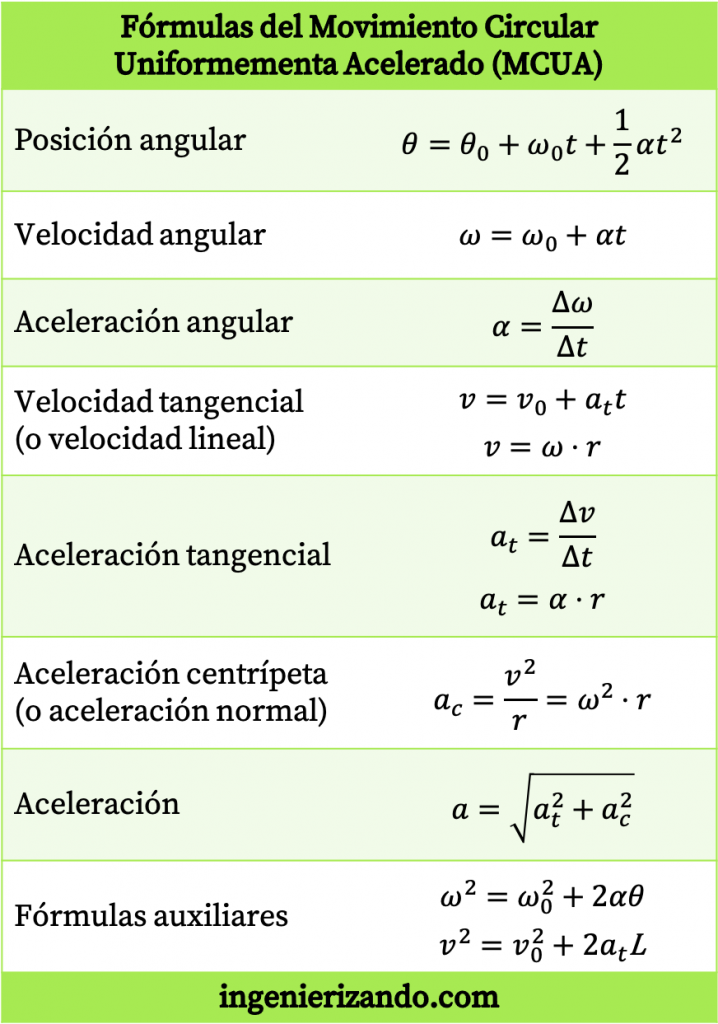
Resumen de las fórmulas del movimiento circular uniformemente acelerado
A modo de resumen, a continuación te dejamos una tabla con todas las fórmulas del movimiento circular uniformemente acelerado (MCUA).

Excelente! Gracias por ser tan explícitos
¡Gracias a ti por comentar Aura!