En este artículo se explica qué son las ondas estacionarias en física. De modo que encontrarás la ecuación de las ondas estacionarias, cuáles son las características de las ondas estacionarias y, además, cuáles son los diferentes tipos de ondas estacionarias.
Índice
¿Qué es una onda estacionaria?
Una onda estacionaria es una perturbación oscilatoria cuyos puntos oscilan verticalmente pero no avanzan longitudinalmente. Las ondas estacionarias son el resultado de la interferencia entre dos o más ondas, que consiste en la superposición de ondas con las mismas características pero que avanzan en sentido opuesto.
En la mayoría de los casos, las ondas estacionarias son debidas al fenómeno físico de la resonancia, de manera que la interferencia entre las ondas se produce entre una onda y su onda reflejada en un medio resonador.
Por ejemplo, cuando atamos una cuerda elástica a una pared por uno de sus extremos y hacemos vibrar la cuerda, se produce una onda estacionaria. La cuerda oscila y las vibraciones se reflejan en el extremo fijo de la cuerda, en consecuencia, las dos ondas se superponen y se forma una onda estacionaria.
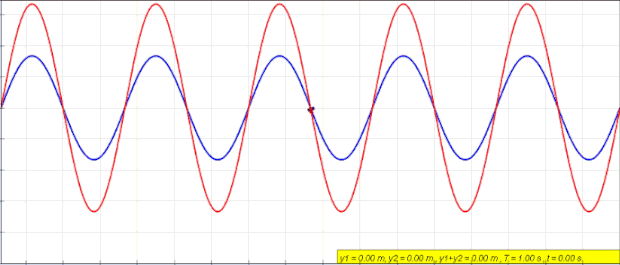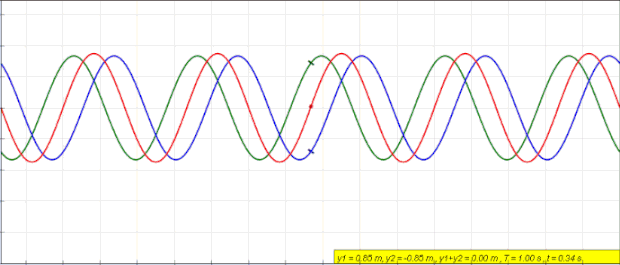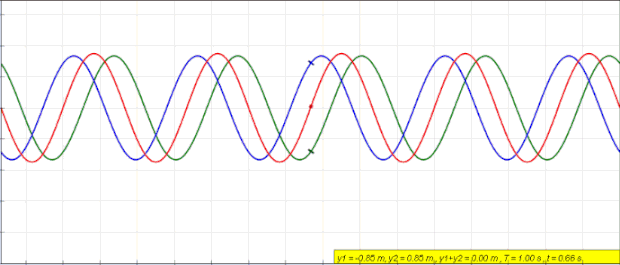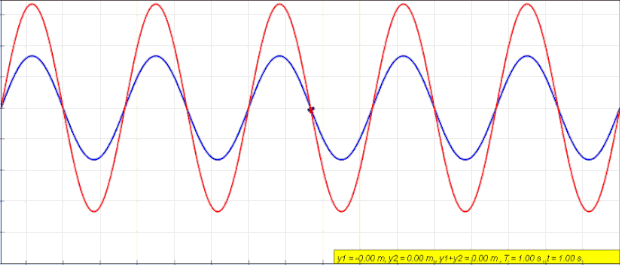
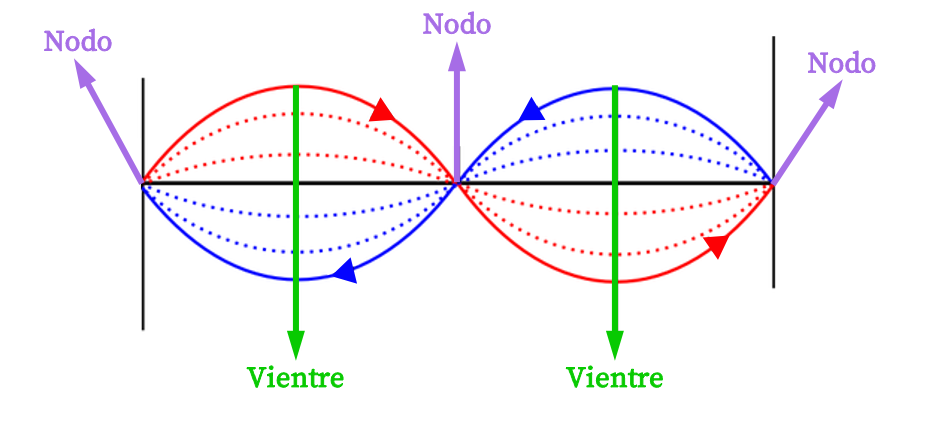
En la gráfica de arriba se ha representado una onda estacionaria (onda de color rojo) junto con las ondas que se superponen para formar la onda estacionaria (ondas de color verde y azul). Como puedes ver, la onda verde avanza hacia la derecha, la onda azul se desplaza hacia la izquierda y, en cambio, la onda estacionaria no se mueve horizontalmente sino que solo vibra verticalmente.
Las ondas estacionarias fueron descritas por primera vez en 1831 por el físico inglés Michael Faraday. No obstante, el nombre de «onda estacionaria» fue establecido en 1860 por el físico alemán Franz Melde.
Ecuación de una onda estacionaria
La ecuación de una estacionaria es dos por la amplitud de las ondas originales por el producto entre el seno del número de onda por la elongación y el coseno de la frecuencia angular por el tiempo. Así pues, la ecuación de una onda estacionaria es y=2·A·sen(k·x)·cos(ω·t).
Donde:
es la elongación del punto estudiado de la onda estacionaria.
es la amplitud de las ondas originales.
es el número de onda.
es la posición del punto estudiado de la onda estacionaria.
es la frecuencia angular o pulsación.
es el instante de tiempo.
Nota: existen varias formas de expresar la ecuación de la onda estacionaria, por lo que según el libro puedes encontrar una ecuación ligeramente diferente. No obstante, en física la ecuación de la onda estacionaria más utilizada es la expuesta en este artículo.
Ten en cuenta que el número de onda y la frecuencia angular de una onda estacionaria se calculan mediante las siguientes fórmulas:
Donde:
es el número de onda.
es la longitud de onda, es decir, la distancia entre dos puntos equivalentes de la onda estacionaria.
es la frecuencia angular o pulsación.
es el periodo, que se define como el tiempo que transcurre desde que la onda pasa por un punto hasta que vuelve a pasar por un punto equivalente.
es la frecuencia, que es el número de oscilaciones de la onda por unidad de tiempo.
Dadas dos ondas de propagación definidas por las siguientes ecuaciones:
La onda estacionaria es la suma de las dos ondas oscilatorias, por lo tanto, la ecuación de la onda estacionaria será la suma de las dos ecuaciones anteriores:
A continuación aplicaremos las siguientes fórmulas trigonométricas:
Así pues, aplicando las fórmulas trigonométricas anteriores llegamos a la ecuación de las ondas estacionarias:
Nodos y vientres de una onda estacionaria
Cualquier onda estacionaria está formada por nodos y vientres, que se definen de la siguiente manera:
- Nodos: son los puntos de la onda estacionaria cuya elongación es mínima (y=0). Estos puntos son completamente estacionarios, ya que no se mueven ni horizontalmente ni verticalmente.
- Vientres (o antinodos): son los puntos de la onda estacionaria cuya elongación es máxima (y=2A o y =-2A). Estos puntos oscilan verticalmente desde la elongación y=2A hasta y=-2A.
Ondas estacionarias con ambos extremos fijos
Cuando se generan ondas estacionarias con los dos extremos fijos significa que los dos extremos de la onda son nodos. Este tipo de ondas estacionarias tienen lugar en tubos cerrados por los dos lados o haciendo vibrar cuerdas fijadas por los extremos.
Por ejemplo, cuando hacemos vibrar las cuerdas de una guitarra estamos generando ondas estacionarias con ambos extremos fijos.
En este caso, la longitud de onda y la frecuencia de la onda estacionaria quedan definidas por la siguientes fórmulas:
Donde:
es la longitud de onda.
es la longitud de la cuerda.
es el número de armónico (n=1, 2, 3, 4…).
es la frecuencia natural o armónica.
es la velocidad de propagación de la onda.
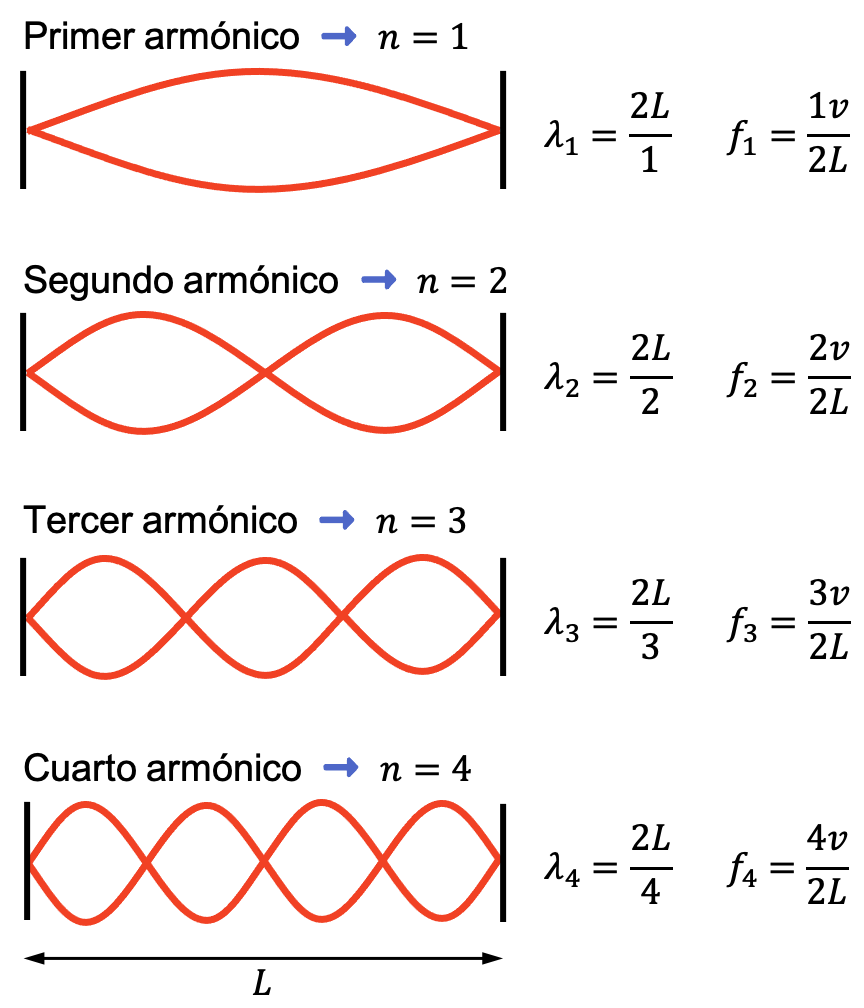
Como puedes ver en la imagen anterior, el número de vientres y el número de nodos depende del número armónico. El número de vientres de una onda estacionaria con los dos extremos fijos es equivalente al número armónico, mientras que el número de nodos es el número armónico más uno.
Ondas estacionarias con ambos extremos libres
Por último, las ondas estacionarias también pueden tener los dos extremos libres, de manera que ambos extremos de la onda estacionaria son vientres.
Este tipo de ondas estacionarias se generan en muchos instrumentos de viento, ya que tienen los dos extremos abiertos.
La longitud de onda y la frecuencia de una onda estacionaria con ambos extremos abiertos se calculan utilizando las siguientes fórmulas:
Donde:
es la longitud de onda.
es la longitud de la cuerda.
es el número armónico (n=1, 2, 3, 4…).
es la frecuencia natural o armónica.
es la velocidad de propagación de la onda.
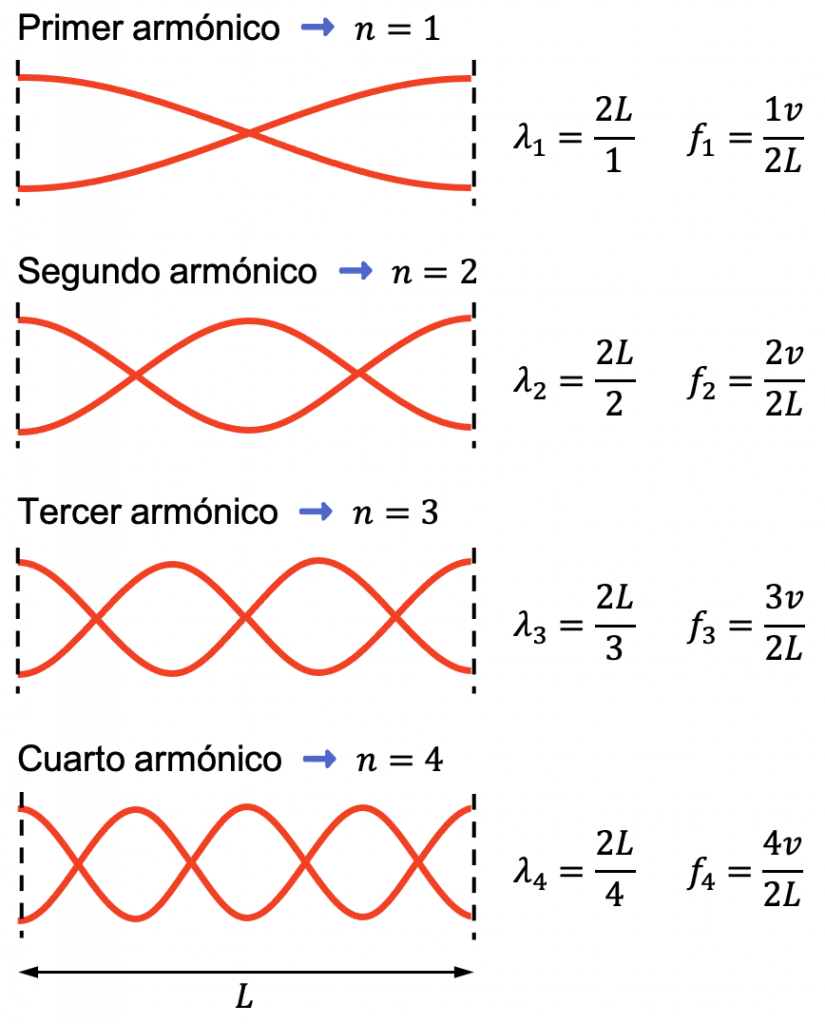
Si te fijas en la imagen de arriba, este tipo de ondas estacionarias tienen tantos nodos como el número armónico. Por otro lado, el número de vientres de esta clase de ondas estacionarias es el número armónico más uno.
Ondas estacionarias con un extremo fijo y un extremo libre
Cuando la onda se propaga en un medio en el que un extremo es fijo y el otro extremo es libre, implica que un extremo de la onda será un nodo y el otro extremo de la onda será un vientre.
Este tipo de ondas estacionarias tienen lugar en muchos instrumentos musicales, por ejemplo, las ondas que se generan en una trompeta, una flauta o un clarinete tienen un extremo fijo, por el que el músico sopla, y otro extremo libre, por el que el sonido sale del instrumento.
En este caso, la longitud y la frecuencia de la onda estacionaria se pueden calcular mediante las siguientes fórmulas:
Donde:
es la longitud de onda.
es la longitud de la cuerda.
es el parámetro que determina el número armónico (n=1, 2, 3, 4…).
es la frecuencia natural o armónica.
es la velocidad de propagación de la onda.
Nota: ten en cuenta que en este caso solo existen los armónicos impares (1, 3, 5, 7…), pues en este tipo de ondas estacionarias solo es posible generar frecuencias múltiples impares de la frecuencia fundamental.
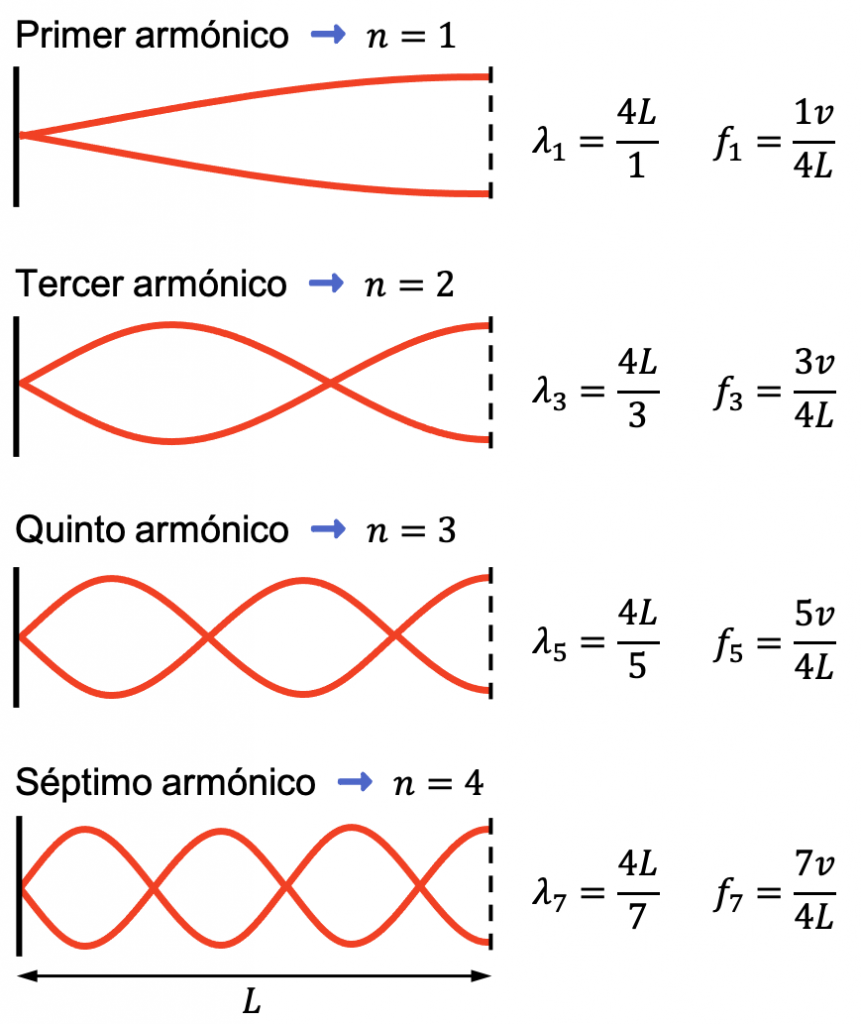
En este caso, la onda estacionaria tiene el mismo número de nodos que de vientres. En concreto, la onda estacionaria tiene tantos nodos y tantos vientres como el valor del parámetro n del armónico:
