En este post se explica qué es un péndulo simple y cuáles son sus características. También se muestran las fórmulas que describen el movimiento de un péndulo simple y, además, podrás ver cuáles son las leyes del péndulo simple.
Índice
¿Qué es un péndulo simple?
El péndulo simple, también llamado péndulo matemático o péndulo ideal, es un sistema compuesto por una partícula con masa que cuelga de un punto fijo mediante un hilo de una determinada longitud.
En física, el péndulo simple se usa para estudiar el movimiento oscilatorio de la masa que cuelga. Si se aplica una fuerza a la masa, esta oscilará yendo de un lado hacia otro pasando por su posición de equilibrio y, por tanto, describirá un movimiento oscilatorio.
En concreto, el movimiento que realiza la masa de un péndulo simple se llama movimiento pendular, el cual se trata de un movimiento periódico ya que la masa pasa por la misma posición cada un intervalo de tiempo fijo.
Características de un péndulo simple
El péndulo simple está definido por las siguientes características o partes:
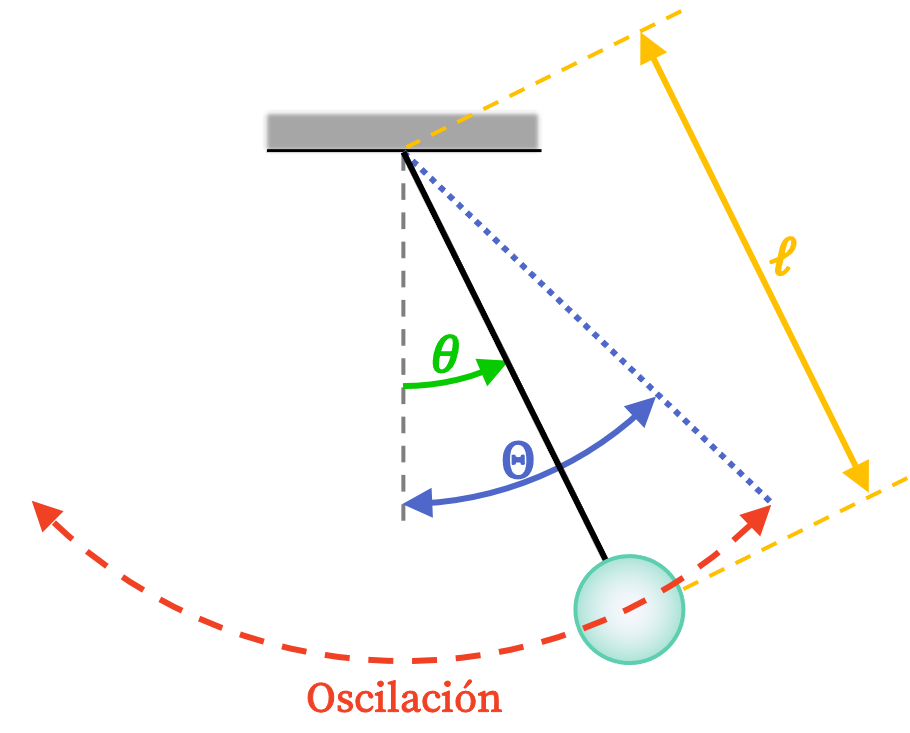
- Longitud (ℓ): es la longitud de la cuerda que va desde el punto fijo del péndulo simple hasta el centro de gravedad del objeto que realiza el movimiento pendular.
- Oscilación: es el arco recorrido por la masa entre las posiciones extremas del péndulo simple más su regreso a su posición inicial.
- Periodo (T): es el tiempo que transcurre en completar una oscilación.
- Frecuencia (f): es el número de oscilaciones que hace el péndulo simple por unidad de tiempo.
- Ángulo (θ): es el ángulo formado por la cuerda del péndulo y la vertical.
- Amplitud (Θ): es el ángulo formado por la vertical y la cuerda del péndulo simple cuando se encuentra en una posición extrema.
Fórmulas del péndulo simple
Ecuación diferencial del péndulo simple
La ecuación diferencial del péndulo simple indica que la suma de la longitud de la cuerda por la aceleración angular más la aceleración de la gravedad por el seno del ángulo que forma la cuerda con la vertical es igual a cero.
Así pues, la ecuación diferencial del péndulo simple es la siguiente:
Donde:
es la longitud del péndulo.
es la aceleración angular.
es el ángulo que forma la cuerda del péndulo con la vertical.
es la aceleración de la gravedad, cuyo valor en la Tierra es 9,81 m/s2.
Si el péndulo simple realiza oscilaciones de pequeña amplitud, se puede hacer la aproximación sen(θ)≈θ. En tal caso, la ecuación diferencial del péndulo simple queda de la siguiente manera:
Ecuación del movimiento del péndulo simple
Al solucionar la ecuación diferencial vista en el apartado de arriba, se llega a la ecuación que describe el ángulo que se ha desplazado el péndulo simple respecto a su posición de equilibrio:
Donde:
es el ángulo formado por la cuerda del péndulo simple y la cuerda.
es la amplitud del péndulo simple.
es la pulsación o frecuencia angular del péndulo simple.
es el instante de tiempo en el que se calcula el ángulo.
es la fase inicial del péndulo simple.
Periodo del péndulo simple
Para oscilaciones pequeñas, el periodo de oscilación de un péndulo simple es igual a dos por pi por la raíz cuadrada del cociente entre la longitud de la cuerda del péndulo y la aceleración de la gravedad.
Por lo tanto, la fórmula para calcular el periodo de oscilación de un péndulo simple con oscilaciones de pequeña amplitud es la siguiente:
Donde:
es el periodo del péndulo simple.
es la longitud de la cuerda del péndulo simple.
es la aceleración de la gravedad, cuyo valor en la Tierra es 9,81 m/s2.
Leyes del péndulo simple
En física, existen cuatro leyes que definen el movimiento oscilatorio de un péndulo simple:
- Ley de la independencia de la masa: dos péndulos cuyas cuerdas miden lo mismo tienen el mismo periodo independientemente de la masa que se cuelgue de las cuerdas. Es decir, dos péndulos con diferentes masas tendrán el mismo periodo si las longitudes de sus cuerdas son iguales.
- Ley del isocronismo: el periodo de un péndulo simple es independiente de la amplitud del movimiento. De modo que si dos péndulos simples tienen la misma longitud de cuerda, sus periodos serán equivalentes aunque sus amplitudes sean diferentes.
- Ley de las longitudes: el periodo de oscilación de un movimiento pendular es proporcional a la longitud de la cuerda del péndulo. Así pues, cuanto mayor sea la longitud de la cuerda, mayor será el periodo del péndulo.
- Ley de las aceleraciones de las gravedades: la aceleración de la gravedad afecta al periodo de oscilación del movimiento del péndulo, por lo que el periodo de un péndulo cambiará según la gravedad del lugar. Cuanto mayor sea la gravedad, menor será el periodo de oscilación del péndulo.

