En este post se explica qué es el vector de posición en física. Así pues, encontrarás cuáles son las propiedades del vector de posición, cómo calcular el vector de posición de un punto y, además, un ejemplo resuelto paso a paso.
Índice
¿Qué es un vector de posición?
Un vector de posición, o simplemente vector posición, es un vector que describe la posición de un punto respecto a un sistema de referencia. Es decir, el vector de posición sirve para indicar la posición de un punto en un sistema de coordenadas.
Matemáticamente, el vector de posición de un punto se define como el vector que va desde el origen de coordenadas hasta ese punto. Por lo tanto, el vector de posición de un punto se calcula restando las coordenadas de dicho punto menos el origen de coordenadas.
En general, el vector de posición se expresa mediante los vectores unitarios 
, 
y 
, que corresponden a las coordenadas de los ejes X, Y y Z respectivamente.
Por ejemplo, si las coordenadas cartesianas de un punto son (3,4,5), el vector de posición de este punto es r=3i+4j+5k.
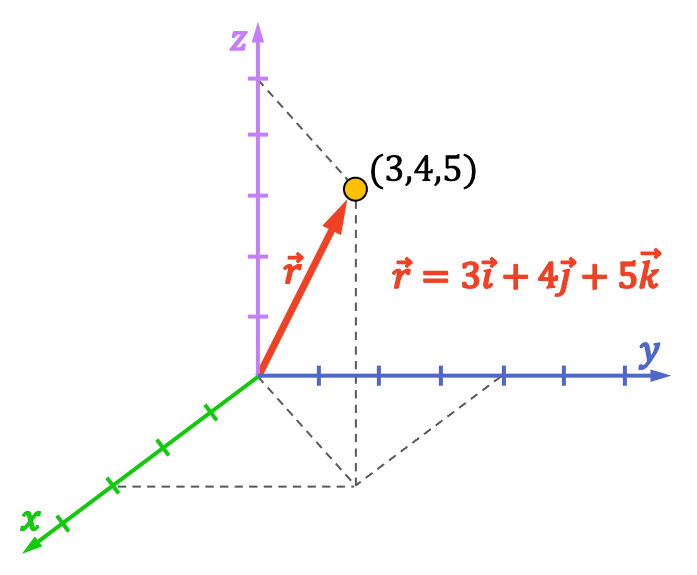
Características del vector de posición
Ahora que ya sabemos la definición del vector de posición, vamos a ver cuáles son sus características.
- El vector de posición de un punto se define como la diferencia entre las coordenadas de dicho punto y el origen de coordenadas. Por lo tanto, la fórmula para calcular el vector de posición de un punto es la siguiente:
- Las coordenadas del vector de posición de un punto se expresan mediante los vectores unitarios , y , que representan las direcciones del eje OX, OY y OZ respectivamente.
- La dirección del vector de posición es la recta que une el origen del sistema de referencia con el punto en cuestión.
- El sentido del vector de posición va desde el origen hasta el punto de estudio.
- El módulo del vector de posición de un punto es la distancia entre el punto y el origen de coordenadas. El módulo del vector de posición es igual a la raíz cuadrada de la suma de los cuadrados de sus coordenadas.
Ten en cuenta que el vector de posición solo tendrá dos coordenadas (x,y) si trabajamos en el plano. En cambio, si trabajamos en el espacio, el vector de posición tendrá tres coordenadas (x,y,z).
Ejercicio resuelto del vector de posición
Para acabar de entender el concepto, a continuación se muestra un ejercicio resuelto sobre cómo se calcula el vector de posición.
- El vector de posición en función del tiempo de un cuerpo está definido por la expresión de abajo. Calcula el vector de posición del cuerpo en el instante t=3 s y su módulo.
Para hallar el vector de posición en el instante t=3 s tenemos que sustituir el parámetro t por su valor y hacer los cálculos:
![\begin{aligned}\vv{r}(3)&=4\cdot 3\vv{i}+2\cdot 3^2\vv{j}+5 \vv{k}\\[2ex]\vv{r}(3)&=12\vv{i}+18\vv{j}+5\vv{k}\end{aligned}](https://www.ingenierizando.com/wp-content/ql-cache/quicklatex.com-4b96c7609bde7d292982ae38f126d7b9_l3.svg "Rendered by QuickLaTeX.com")
Luego sacamos el módulo del vector de posición calculando la raíz cuadrada de la suma de los cuadrados de las coordenadas:
![\begin{aligned}|\vv{r}(3)|&=\sqrt{12^2+18^2+5^2}\\[2ex]|\vv{r}(3)|&=\sqrt{493}\end{aligned}](https://www.ingenierizando.com/wp-content/ql-cache/quicklatex.com-78aa2e100fe4f15edea87c99fafcd58d_l3.svg "Rendered by QuickLaTeX.com")
Vector de posición y desplazamiento
El desplazamiento de un punto se define como la distancia entre el punto final y el punto inicial. Por lo tanto, el vector desplazamiento es el vector que se obtiene de restar el vector de posición final menos el vector de posición inicial.
Por lo tanto, la diferencia entre el vector de posición y el desplazamiento es que el vector de posición indica la posición de un cuerpo en un instante de tiempo determinado, en cambio, el vector desplazamiento indica la distancia entre dos posiciones diferentes de un cuerpo móvil.
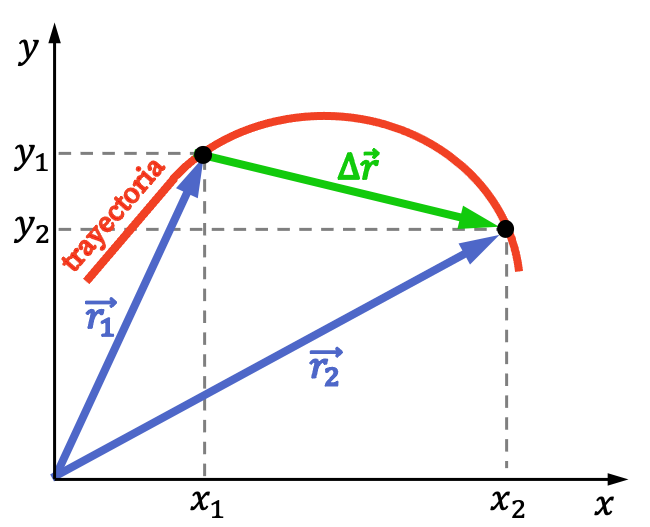
Asimismo, se debe diferenciar el desplazamiento del recorrido. El recorrido se refiere a la longitud de toda la trayectoria recorrida, mientras que el desplazamiento se refiere a la distancia entre la posición final y la posición final. De modo que el recorrido puede ser más grande que el desplazamiento.
