▷ Cómo calcular las componentes de una fuerza (ejemplos)

En este artículo se explica qué son las componentes de una fuerza y cómo se calculan. Además, podrás ver ejemplos resueltos del cálculo de las componentes de fuerzas.

Índice

¿Qué son las componentes de una fuerza?

Las componentes de una fuerza son las proyecciones de una fuerza sobre los ejes de referencia. Si trabajamos en el sistema de coordenadas cartesianas, una fuerza tiene dos componentes: la componente sobre el eje X y la componente sobre el eje Y.

Normalmente, las fuerzas están aplicadas sobre el sistema de coordenadas cartesianas, por lo que las dos componentes de una fuerza en el plano se suelen llamar la componente horizontal y la componente vertical de la fuerza.

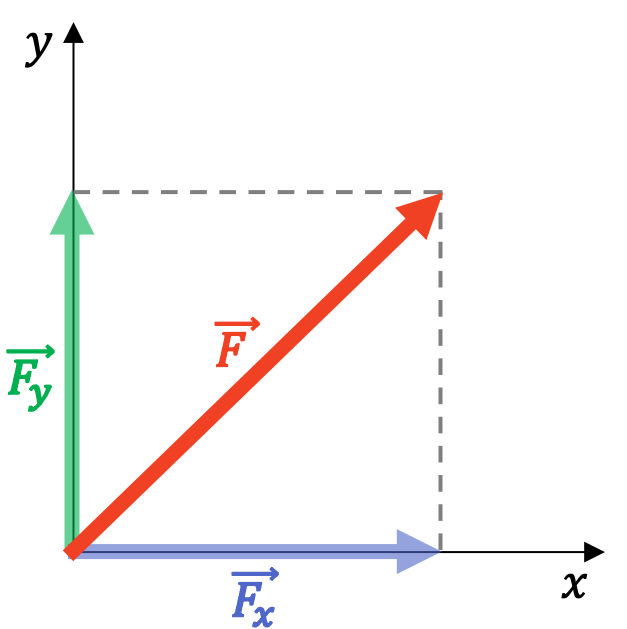
Ten presente que a veces se utilizan los vectores unitarios $\vv{i}$ y $\vv{j}$ para expresar las componentes rectangulares de una fuerza de otra manera:

$\vv{F}=\vv{F_x}+\vv{F_y}=F_x\cdot \vv{i}+F_y\cdot \vv{j}$

Cómo calcular las componentes de una fuerza

Las componentes rectangulares de una fuerza se calculan utilizando las razones trigonométricas del seno y del coseno.

La componente horizontal de una fuerza es igual al módulo de la fuerza por el coseno del ángulo de inclinación de la fuerza.
La componente vertical de una fuerza es igual al módulo de la fuerza por el seno del ángulo de inclinación de la fuerza.

Ver demostración

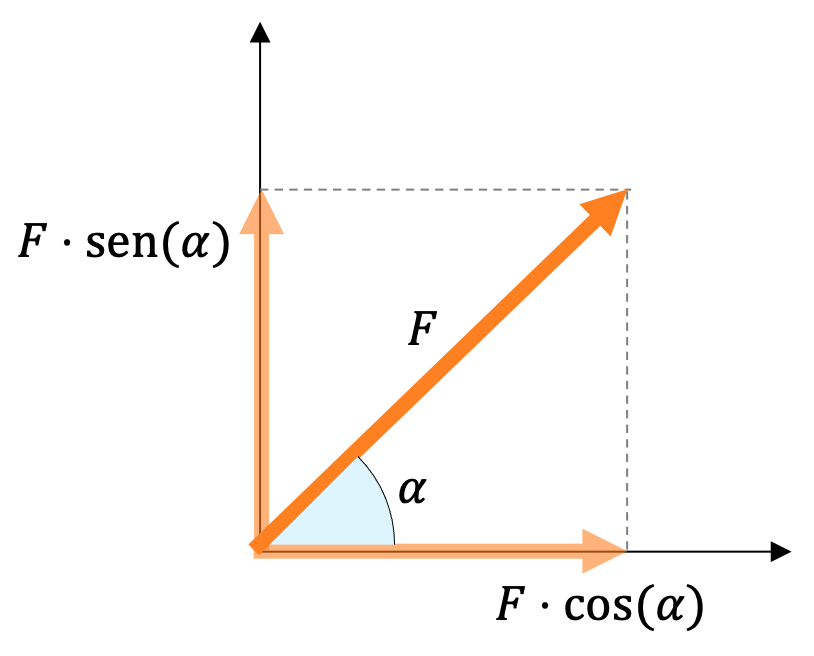
Cualquier fuerza vectorial hace un triángulo rectángulo junto con sus componentes vectoriales, por lo tanto, podemos relacionar el módulo con las componentes aplicando las razones trigonométricas.

El coseno de un ángulo es igual al cateto continuo partido por la hipotenusa del triángulo rectángulo, en nuestro caso la hipotenusa es el módulo de la fuerza y la componente horizontal el lado continuo:

$\text{cos}(\alpha)=\cfrac{F_x}{F}$

De manera que de la relación matemática anterior podemos despejar la componente X de la fuerza:

$F_x=F\cdot \text{cos}(\alpha)$

Por otra parte, podemos aplicar el mismo razonamiento para obtener la fórmula de la componente Y de la fuerza pero utilizando el seno.

El seno de un ángulo es igual al cateto opuesto partido por la hipotenusa del triángulo rectángulo, en nuestro caso la hipotenusa es el módulo de la fuerza y la componente vertical el lado opuesto al ángulo:

$\text{sen}(\alpha)=\cfrac{F_y}{F}$

Y finalmente despejamos la componente Y de la fuerza:

$F_y=F\cdot \text{sen}(\alpha)$

Al proceso de determinar las componentes vectoriales de una fuerza se llama descomposición vectorial de una fuerza.

Ten en cuenta que si el ángulo que conocemos no es el que forman la fuerza con el eje horizontal las fórmulas cambiarán. Por ejemplo, si solo sabemos el ángulo que forma la fuerza con el eje vertical, entonces debemos usar el coseno para la componente vertical y el seno para la componente horizontal.

Ejemplos de componentes de fuerzas

Ahora que ya conocemos la definición, vamos a ver dos ejercicios resueltos de cómo sacar las componentes de una fuerza.

Ejemplo 1

¿Cuáles son las componentes cartesianas de una fuerza de 8 N inclinada 35º respecto el eje horizontal?

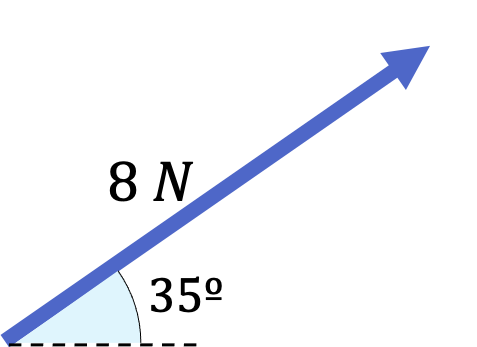
ejemplo resuelto de descomposicion vectorial de una fuerzaz

Para descomponer vectorialmente la fuerza simplemente debemos utilizar las fórmulas del seno y del coseno vistas más arriba.

La componente horizontal es el valor de la fuerza multiplicada por el coseno del ángulo:

$F_{x}=F\cdot \text{cos}(\alpha)$

$F_{x}=8\cdot \text{cos}(35º)=6,55 \ N$

Y la componente vertical es la intensidad de la fuerza multiplicada por el seno del ángulo:

$F_{y}=F\cdot \text{sen}(\alpha)$

$F_{y}=8\cdot \text{sen}(35º)=4,59 \ N$

Ejemplo 2

Halla las componentes vectoriales de la fuerza gravitatoria del peso que actúa sobre el siguiente cuerpo de 5 kg en los ejes 1-2 representados.

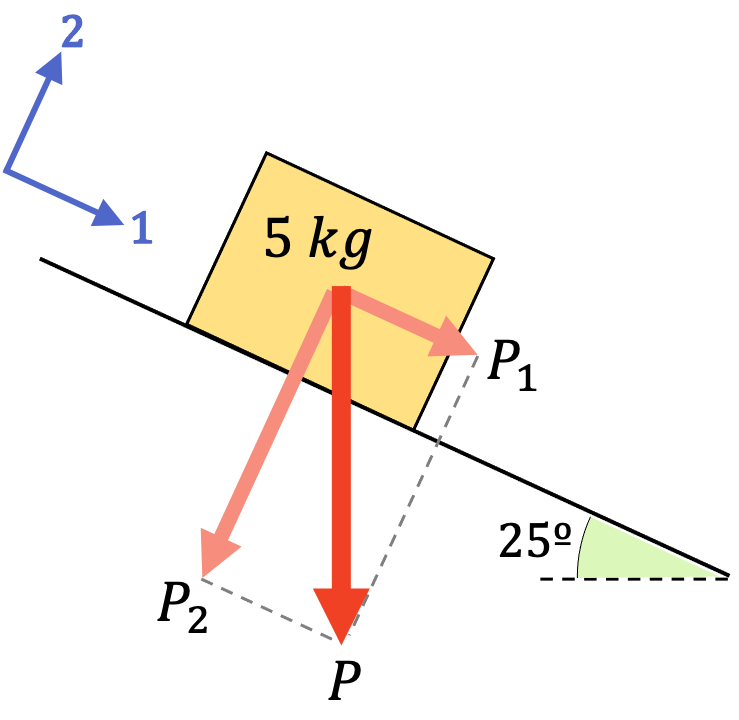
ejercicio resuelto de las componentes de una fuerza

En primer lugar, tenemos que encontrar el valor de la fuerza del peso, por lo tanto, utilizamos su fórmula correspondiente:

$P=m\cdot g= 5\cdot 9,81=49,05 \ N$

Y ahora que ya sabemos cuánto es el valor de la fuerza, podemos determinar sus componentes rectangulares. El ángulo entre la componente P₂ y la fuerza P es equivalente al ángulo de la pendiente, de modo que podemos emplear las fórmulas de las componentes con ese ángulo:

$P_{1}=P\cdot \text{sen}(25º)=49,05\cdot \text{sen}(25º)=20,73 \ N$

$P_{2}=-P\cdot \text{cos}(25º)=-49,05\cdot \text{cos}(25º)=-44,45 \ N$

La componente P₂ es negativa porque su sentido es contrario al sentido del eje.

Composición de una fuerza

Si has llegado hasta aquí significa que ya sabes cómo se calculan las componentes de una fuerza. Pues ahora vamos a ver el proceso inverso, es decir, cómo determinar el módulo de una fuerza a partir sus componentes rectangulares.

Para hallar la magnitud de una fuerza (o módulo de una fuerza) tenemos que calcular la raíz cuadrada de la suma de los cuadrados de las componentes de dicha fuerza.

$\begin{vmatrix}\vv{F}\end{vmatrix}=\sqrt{F_x^2+F_y^2}$

➤ Ver: ¿qué es la magnitud de una fuerza?

A este proceso se le llama composición de una fuerza.

Por ejemplo, si la componente horizontal de una fuerza es de 6 N y su componente vertical es de 8 N, el módulo de la fuerza será:

$\begin{aligned}\begin{vmatrix}\vv{F}\end{vmatrix} & =\sqrt{F_x^2+F_y^2}\\[2ex]& =\sqrt{6^2+8^2}\\[2ex] & = \sqrt{100} \\[2ex] & = 10 \ N \end{aligned}$

Es importante tener en cuenta que esta fórmula solamente se puede utilizar si las dos fuerzas forman un ángulo de 90º. De lo contrario, para hallar la fuerza resultante de unir dos fuerzas con un ángulo diferente se deben aplicar otros métodos (dependiendo del caso), puedes ver cómo se hace en nuestra página web.

Componentes de una fuerza