En este artículo se explica qué es el equilibrio mecánico junto con varios ejemplos. También encontrarás los diferentes tipos de equilibrio y, además, podrás practicar con un ejercicio resuelto paso a paso.
Índice
¿Qué es el equilibrio mecánico?
El equilibrio mecánico es un estado estacionario en el que se encuentra un cuerpo cuando la suma de fuerzas y de momentos aplicados sobre él es igual a cero.
Por lo tanto, un sistema debe cumplir dos condiciones para encontrarse en equilibrio. La primera condición de equilibrio establece que el sumatorio de fuerzas de cada eje debe ser nulo.
Del mismo modo, la segunda condición de equilibrio dice que el sumatorio de momentos de cada eje debe dar como resultado cero para que se considere que el sistema está en equilibrio.
Cuando se cumplen estas dos reglas del equilibrio significa que el cuerpo no tiene ni aceleración lineal ni aceleración angular. En consecuencia, el cuerpo está en reposo, se mueve a velocidad lineal constante, o gira a velocidad angular constante.
En física, cuando un cuerpo está en equilibrio mecánico también se dice que está en equilibrio traslacional y rotacional o que simplemente está en equilibrio.
Esta es una manera de explicar en qué consiste el equilibrio mecánico, la más sencilla desde mi punto de vista, pero más abajo veremos otra forma de definir el equilibrio mecánico.
Ejemplos de equilibrio mecánico
Vista la definición de equilibrio mecánico, a continuación puedes varios ejemplos de equilibrios mecánicos para entender mejor el concepto.
- Un ejemplo de equilibrio mecánico es una lámpara que se sostiene colgada del techo. La lámpara está en reposo ya que la fuerza que se hace para aguantarla contrarresta la fuerza de su peso, por lo tanto, está en una posición de equilibrio mecánico.
- Otro ejemplo de equilibrio mecánico es una balanza. Cuando el brazo de la balanza deja de girar significa que la suma de momentos aplicados sobre él es cero, por lo que se encuentra en equilibrio mecánico.
- Como último ejemplo de equilibrio mecánico podemos poner un coche que avanza a velocidad constante. Si el coche avanza a velocidad constante quiere decir que su aceleración es nula y, por lo tanto, la suma de fuerzas y momentos también. De modo que está en equilibrio mecánico.
Tipos de equilibrios
Dentro del equilibrio mecánico, hay tres tipos de equilibrios diferentes: el equilibrio estable, el equilibrio inestable y el equilibrio indiferente.
- Equilibrio estable: un cuerpo está en equilibrio estable cuando vuelve a su posición original después de ser desplazado. Por ejemplo un péndulo.
- Equilibrio inestable: un cuerpo está en equilibrio inestable cuando no encuentra ninguna posición de equilibrio después de que una fuerza lo aparte. Por ejemplo un lápiz sostenido verticalmente.
- Equilibrio indiferente (o equilibrio neutral): un cuerpo está en equilibrio indiferente si cuando pierde su posición de equilibrio encuentra otra nueva posición de equilibrio distinta. Por ejemplo una canica situada en el suelo.
Relación del equilibrio mecánico con la energía potencial
Como veremos a continuación, el equilibrio mecánico está relacionado matemáticamente con la energía potencial. De manera que el significado de equilibrio mecánico también se puede explicar mediante la energía potencial, aunque es un poco más difícil de entender.
Un sistema está en equilibrio mecánico en un punto cuando la primera derivada de la energía potencial en dicho punto es igual a cero.
Asimismo, según el signo de la segunda derivada se puede distinguir qué tipo de equilibrio se trata:
- Equilibrio estable: un punto es de equilibrio estable si la segunda derivada de la energía potencial en ese punto es positiva. Es decir, si la función de la energía potencial tiene un mínimo en ese punto.
- Equilibrio inestable: un punto es de equilibrio inestable cuando la segunda derivada de la energía potencial en ese punto es negativa. Esto es, si la función de la energía potencial tiene un máximo en ese punto.
- Equilibrio indiferente: un punto es de equilibrio indiferente cuando la segunda derivada de la energía potencial en ese punto es nula.
Ejercicio resuelto del equilibrio mecánico
Calcula la fuerza que debe hacer cada plano inclinado para sostener el siguiente cilindro de masa 25 kg en equilibrio mecánico. Neglige el rozamiento en todo el ejercicio.
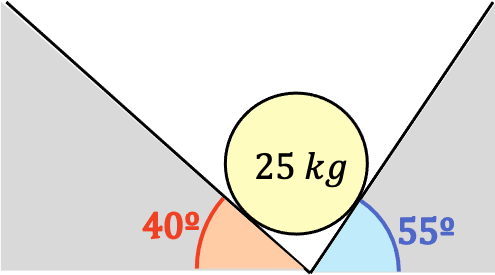
Como en todos los problemas de estática, para resolver un problema primero tenemos que hacer el diagrama de cuerpo libre del sistema:
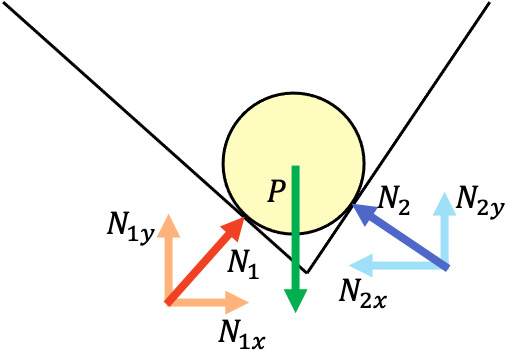
Ten en cuenta que las fuerzas representadas N1x, N1y y N2x, N2y son las componentes de las fuerzas N1 y N2 respectivamente.
Entonces, para que el sistema esté en equilibrio mecánico, se deben cumplir las siguientes dos ecuaciones:
De la primera ecuación podemos deducir que las fuerzas de los dos planos tienen la siguiente relación:
Ahora sustituimos las variables de la segunda ecuación por sus expresiones:
Y sustituimos la relación hallada en la primera ecuación para encontrar el valor de la fuerza N2:
Y, finalmente, sustituimos el valor encontrado en la relación entre fuerzas para determinar N1:
