En este artículo se explica en qué consiste la fuerza normal y cómo determinar la fuerza normal según el tipo de problema. De modo que encontrarás las características de la fuerza normal y, además, podrás practicar con ejercicios resueltos paso a paso de este tipo de fuerza.
Índice
¿Qué es la fuerza normal?
En física, la fuerza normal es una fuerza que ejerce una superficie sobre un cuerpo apoyado sobre ella. Por lo tanto, la dirección de la fuerza normal es perpendicular a la superficie y el sentido de la fuerza normal es hacia afuera, es decir, la superficie aplica la fuerza normal hacia el cuerpo.
En general, la fuerza normal sirve para contrarrestar la fuerza del peso, que es la fuerza de atracción gravitatoria que ejerce la Tierra sobre cualquier cuerpo con masa. No obstante, cuando el cuerpo se encuentra apoyado sobre una superficie inclinada, el valor de la fuerza normal puede no ser suficiente. Más abajo veremos cómo se calcula la fuerza normal en un plano inclinado.
En definitiva, las características de las fuerza normal son:
- La fuerza normal es una fuerza de contacto, es decir, solo se puede aplicar si dos superficies están en contacto.
- La dirección de la fuerza normal es perpendicular a la superficie sobre la que está apoyada el cuerpo.
- El sentido de la fuerza normal siempre es hacia afuera, pues es la superficie la que aplica la fuerza normal sobre el cuerpo.
- En general, el módulo de la fuerza normal es equivalente a la proyección de la fuerza resultante sobre la superficie de apoyo.
- Normalmente la fuerza normal se suele representar mediante el símbolo N o FN.
Cómo calcular la fuerza normal
En general, para calcular la fuerza normal se deben aplicar las ecuaciones de equilibrio, las cuales establecen que un cuerpo está en equilibrio cuando el sumatorio de fuerzas verticales y el sumatorio de fuerzas horizontales son iguales a cero.
Al aplicar las condiciones de equilibrio sobre el problema, podremos despejar la fuerza normal de las ecuaciones planteadas y, por lo tanto, determinar el valor de la fuerza normal.
![\begin{array}{c}\displaystyle\sum \vv{F_x}=0\\[2ex]\displaystyle\sum \vv{F_y}=0\end{array}](https://www.ingenierizando.com/wp-content/ql-cache/quicklatex.com-82c4f71bd35b2b3600a528fbb355874d_l3.svg "Rendered by QuickLaTeX.com")
Ejemplo del cálculo de la fuerza normal
Ahora que ya sabemos la definición de fuerza normal, vamos a ver un ejemplo resuelto del cálculo de la fuerza normal.
- Un cuerpo con una masa de 8 kg se encuentra en reposo sobre un suelo plano. ¿Cuál es el valor de la fuerza normal que ejerce el suelo sobre el cuerpo?
En este problema, el cuerpo se encuentra en reposo sobre una superficie plana, por lo tanto, las únicas fuerzas que actúan sobre él son la fuerza del peso y la fuerza normal.
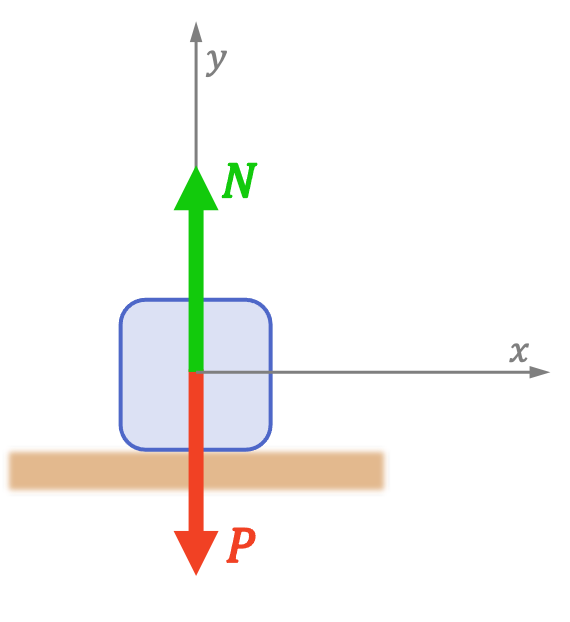
Entonces, para que un cuerpo se encuentre en equilibrio sobre una superficie plana, el módulo de la fuerza normal (N) y de la fuerza del peso (P) deben ser iguales. Por lo tanto, la normal y el peso tienen la misma dirección, el mismo módulo pero su sentido es opuesto.
Así pues, para determinar el valor de la fuerza normal simplemente tenemos que calcular el peso del cuerpo, que es equivalente a su masa por la aceleración de la gravedad:
Fuerza normal en un plano inclinado
En este apartado deduciremos la fórmula de la fuerza normal en un plano inclinado, ya que su valor cambia según si la superficie es plana o inclinada.
Así pues, las fuerzas que actúan sobre un cuerpo apoyado en un plano inclinado son las siguientes:
Fíjate en la figura de arriba que cuando el plano está inclinado es más conveniente utilizar como ejes la dirección paralela al plano (eje 1) y la dirección perpendicular al plano (eje 2). De este modo resulta más fácil plantear las ecuaciones de equilibrio.
Para calcular la fuerza normal en un plano inclinado se debe aplicar la condición de equilibrio en el eje perpendicular al plano inclinado, ya que se puede garantizar que el cuerpo está en equilibrio en este eje pero no en el eje paralelo al plano.
De manera que la fuerza normal en un plano inclinado es equivalente a la componente del peso del eje perpendicular al plano:
La componente del peso del eje perpendicular al plano es igual a la fórmula del peso multiplicado por el coseno del ángulo de inclinación del plano:
En definitiva, la fórmula de la fuerza normal en un plano inclinado establece que la fuerza normal es igual a la masa del cuerpo por la gravedad por el coseno del ángulo de inclinación del plano:
Fuerza normal y fuerza de rozamiento
En este apartado veremos la relación entre la fuerza normal y la fuerza de rozamiento, ya que son dos tipos de fuerzas relacionadas matemáticamente. Pero antes, debes saber en qué consiste la fuerza de rozamiento.
La fuerza de rozamiento (o fuerza de fricción) es una fuerza que aparece cuando se intenta mover un cuerpo por una superficie no lisa. De manera que la fuerza de rozamiento es una fuerza que va en contra del movimiento de un cuerpo.
La fuerza de rozamiento se calcula a partir de la fuerza normal. En concreto, la fuerza de rozamiento es igual al coeficiente de fricción de la superficie por la fuerza normal.
Donde:
es la fuerza de rozamiento.
es el coeficiente de fricción.
es la fuerza normal.
Ejercicios resueltos de la fuerza normal
Ejercicio 1
Un cuerpo de masa 5 kg se encuentra en reposo sobre un suelo plano. Si luego se añade otro cuerpo de masa 3 kg encima del primer cuerpo, ¿cuál es la fuerza normal que hace el suelo para sostener los dos cuerpos? Datos: g=9,81 m/s2.
Como el suelo debe sostener los dos cuerpos, la fuerza normal será la suma de la fuerza del peso de cada cuerpo. Por lo tanto, primero calcularemos el peso de cada cuerpo y luego los sumaremos.
Recuerda que la fuerza del peso se calcula multiplicando la masa del cuerpo por la gravedad.
Así pues, calculamos el peso del cuerpo de masa 5 kg:
En segundo lugar, determinamos el peso del segundo cuerpo cuya masa es de 3 kg:
De modo que al aplicar la condición de equilibrio vertical, se obtiene que la fuerza normal es equivalente a la suma de los dos pesos:
En conclusión, el valor de la fuerza normal que ejerce el suelo es:
Ejercicio 2
Tal y como se ve en la siguiente figura, dos cuerpos están conectados por una cuerda y una polea de masas despreciables. Si el cuerpo 2 tiene una masa m2=7 kg y la inclinación de la rampa es de 50º, calcula la fuerza normal que ejerce el plano inclinado sobre el cuerpo de masa m1 para que todo el sistema esté en equilibrio. Desprecia la fuerza de rozamiento en todo el ejercicio.
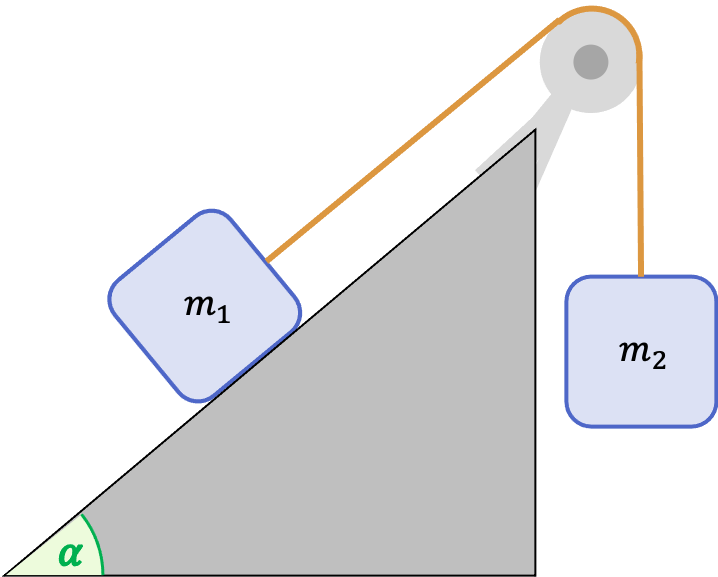
El cuerpo 1 está sobre una pendiente inclinada, por lo tanto, lo primero que debemos hacer es descomponer vectorialmente la fuerza de su peso para tener las fuerzas en los ejes de la pendiente:
De modo que el conjunto de fuerzas que actúan en todo el sistema son:
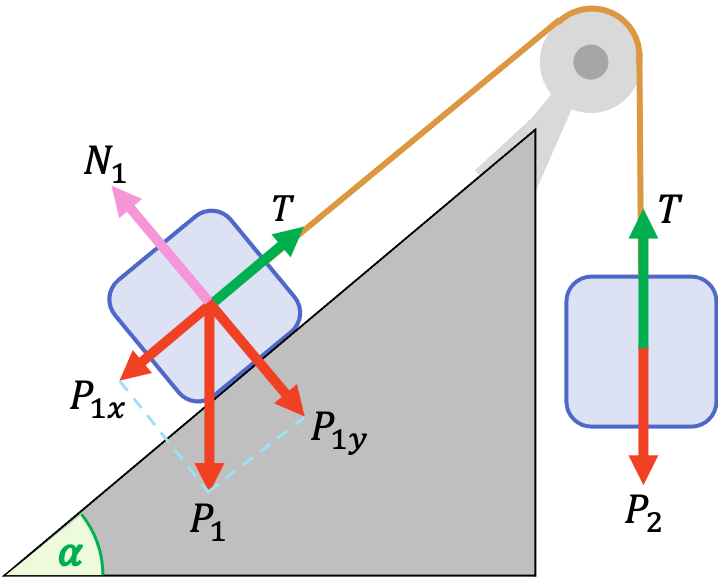
El enunciado del problema nos dice que el sistema de fuerzas está en equilibrio, por lo que los dos cuerpos deben estar en equilibrio. A partir de esta información podemos plantear las ecuaciones de equilibrio de los dos cuerpos:
![1\ \rightarrow \ \begin{cases}P_{1x}=T\\[2ex]P_{1y}=N\end{cases} \qquad\qquad 2 \ \rightarrow \ T=P_2](https://www.ingenierizando.com/wp-content/ql-cache/quicklatex.com-bc78435adf7fa8b1ff18079f501c5863_l3.svg "Rendered by QuickLaTeX.com")
Por lo tanto, la componente vectorial del peso del cuerpo 1 inclinada en el sentido de la pendiente debe ser igual al peso del objeto 2.
De la ecuación anterior podemos calcular la masa del cuerpo 1:
Por otro lado, si nos fijamos en el diagrama de fuerzas del sistema, observamos que la fuerza normal debe ser igual a la componente vectorial del peso del cuerpo 1 perpendicular al plano inclinado.
Así pues, de esta ecuación podemos hallar el valor de la fuerza normal:
![\begin{array}{l}N=P_1\cdot \text{cos}(\alpha)\\[3ex]N=m_1 \cdot g\cdot \text{cos}(\alpha)\\[3ex]N=9,14 \cdot 9,81 \cdot \text{cos}(50\text{º})\\[3ex]N=\bm{57,63 \ N}\end{array}](https://www.ingenierizando.com/wp-content/ql-cache/quicklatex.com-1f0011c81df9d611eecf9922b31388f0_l3.svg "Rendered by QuickLaTeX.com")
Ejercicio 3
Colocamos un cuerpo de masa m=2 kg encima de una rampa con un ángulo de inclinación de 30º. ¿Cuál es el coeficiente de fricción entre la rampa y el cuerpo si se mantiene en equilibrio? Datos: g=9,81 m/s2
Como en cualquier problema de física sobre fuerzas, lo primero que debemos hacer es dibujar el diagrama de cuerpo libre del sistema. Así pues, todas las fuerzas que actúan en este sistema son:
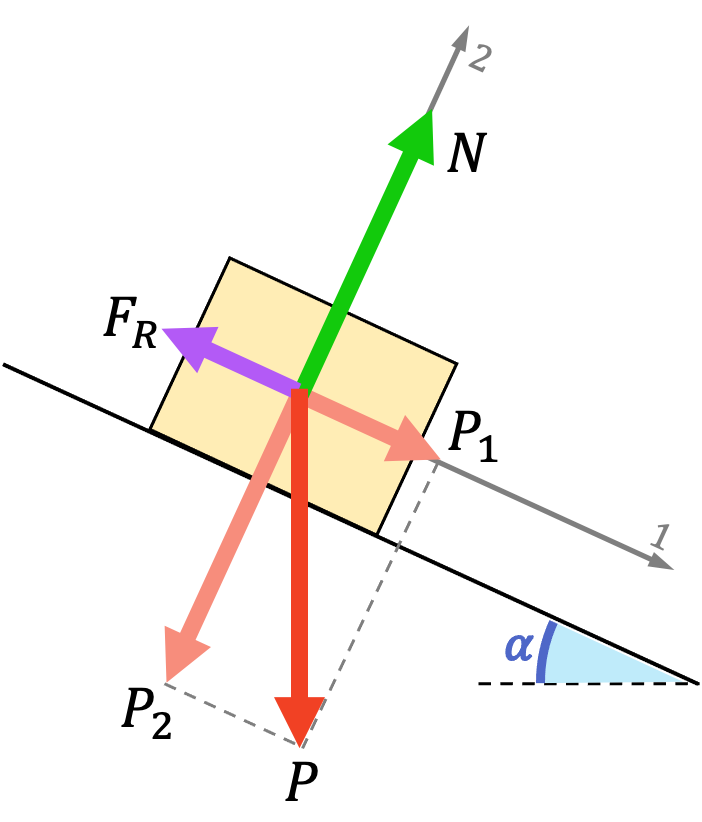
Entonces, para que el sistema esté en equilibrio, el sumatorio de fuerzas en los ejes 1 y 2 deben ser iguales a cero. Por lo tanto, se cumplen la siguientes ecuaciones:
Ahora podemos calcular el valor de la fuerza normal a partir de la segunda ecuación:
![\begin{array}{l}N=P_2\\[3ex]N=P\cdot \text{cos}(\alpha)\\[3ex]N=m \cdot g\cdot \text{cos}(\alpha)\\[3ex]N=2 \cdot 9,81 \cdot \text{cos}(30\text{º})\\[3ex]N=16,99 \ N\end{array}](https://www.ingenierizando.com/wp-content/ql-cache/quicklatex.com-7b7e623ff2c1d4056bc9e68e56dbe827_l3.svg "Rendered by QuickLaTeX.com")
Por otro lado, determinamos el valor de la fuerza de rozamiento utilizando la primera ecuación:
![\begin{array}{l}F_R=P_1\\[3ex]N=P\cdot \text{sen}(\alpha)\\[3ex]F_R=m \cdot g\cdot \text{sen}(\alpha)\\[3ex]F_R=2 \cdot 9,81 \cdot \text{sen}(30\text{º})\\[3ex]F_R=9,81 \ N\end{array}](https://www.ingenierizando.com/wp-content/ql-cache/quicklatex.com-6fb5cb4006c4288d0cf106840ed7755b_l3.svg "Rendered by QuickLaTeX.com")
Asimismo, la fuerza de rozamiento se puede relacionar con la fuerza normal y el coeficiente de fricción mediante la siguiente fórmula:
De modo que despejamos el coeficiente de fricción de la ecuación y calculamos su valor:
