En este artículo te explicamos cuáles son las tres leyes de Kepler y para qué sirven. Primero encontrarás un breve resumen de las leyes de Kepler y, posteriormente, las leyes de Kepler explicadas más detalladamente.
Índice
¿Cuáles son las leyes de Kepler?
Las leyes de Kepler son:
- Primera ley de Kepler: los planetas que se mueven alrededor del Sol describen órbitas elípticas, el Sol se encuentra en uno de los focos de la elipse.
- Segunda ley de Kepler: los planetas barren áreas iguales en tiempos iguales.
- Tercera ley de Kepler: el cuadrado del periodo orbital de un planeta es proporcional al cubo de su distancia media al Sol.
A continuación puedes ver una explicación más detallada de cada ley de Kepler junto con ejemplos para entender mejor el significado de cada ley.
Primera ley de Kepler
La primera ley de Kepler (o ley de las órbitas) dice que todos los planetas que giran alrededor del Sol describen una trayectoria elíptica, es decir, sus órbitas tienen forma de elipse. Además, la primera ley de Kepler especifica que el Sol se sitúa en uno de los focos de la elipse descrita.
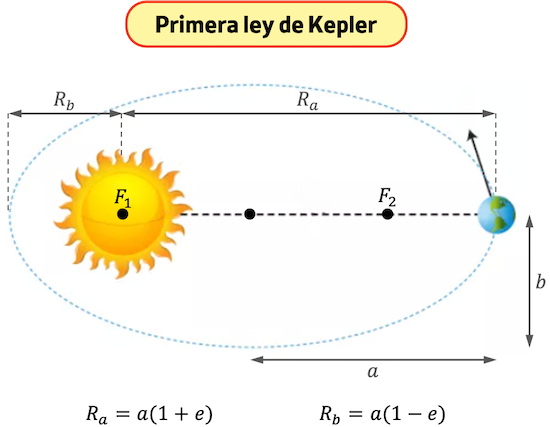
Esta ley significa que la distancia del planeta al Sol está cambiando constantemente, ya que el radio de la elipse va variando y, además, el Sol no está en el centro de la elipse.
La excentricidad de una elipse es una medida que indica cuánto de alejados están los focos de una elipse de su centro. La fórmula para calcular la excentricidad de una elipse es la siguiente:
La mayoría de las órbitas planetarias tienen un valor de excentricidad muy cercano al 0, por lo que a nivel práctico se pueden considerar como círculos descentrados. Puedes ver el valor de la excentricidad de la trayectoria elíptica que hace cada planeta del Sistema Solar en la siguiente tabla:
| Planeta | Excentricidad de la órbita |
|---|---|
| Mercurio | 0,206 |
| Venus | 0,0068 |
| Tierra | 0,0167 |
| Marte | 0,0934 |
| Júpiter | 0,0485 |
| Saturno | 0,0556 |
| Urano | 0,0472 |
| Neptuno | 0,0086 |
Segunda ley de Kepler
La segunda ley de Kepler (o ley de las áreas) dice que los planetas orbitan alrededor del Sol con una velocidad areolar constante. Es decir, la segunda ley de Kepler afirma que la recta imaginaria que va desde el planeta hasta el Sol barre áreas iguales en tiempos iguales.
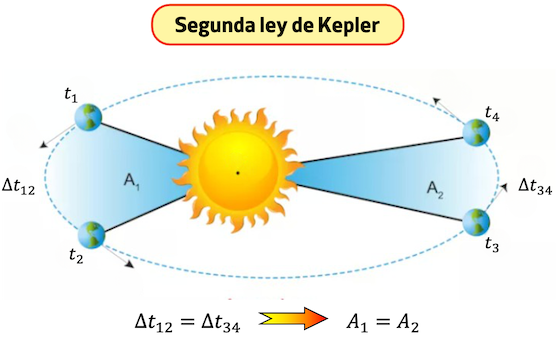
Para que se cumpla la segunda ley de Kepler, la velocidad del planeta debe aumentar a medida que se acerca al Sol.
Dos conceptos relacionados con esta ley de Kepler son el perihelio y el afelio:
- Perihelio: es el punto de la órbita de un planeta más próximo al Sol.
- Afelio: es el punto de la órbita de un planeta más lejano al Sol.
De manera que cualquier planeta que orbita alrededor del Sol consigue su velocidad máxima en el perihelio, mientras que alcanza la velocidad mínima cuando está en el afelio.
A partir de la segunda ley de Kepler, podemos deducir que se conserva el momento angular, de modo que el producto de la masa del planeta por el producto vectorial entre el radio de la trayectoria y la velocidad del planeta es constante. En definitiva, se cumplen las siguientes ecuaciones:
Donde:
es el momento angular.
es la masa del planeta.
es la distancia del planeta al Sol en el instante de tiempo i.
es la velocidad del planeta en el instante de tiempo i.
Tercera ley de Kepler
La tercera ley de Kepler (o ley de los periodos) relaciona el periodo orbital de los planetas con su radio de trayectoria medio. En concreto, la tercera ley de Kepler dice que el cuadrado del periodo orbital de un planeta es proporcional al cubo de la distancia media de dicho planeta al Sol (T2=k·r3).
Por lo tanto, la fórmula de la tercera ley de Kepler es la siguiente:
Donde:
es el periodo orbital del planeta, es decir, el tiempo que tarda en hacer una vuelta alrededor del Sol.
es la constante de proporcionalidad característica de cada planeta, cuya unidad en el Sistema Internacional es s2/m3.
es la distancia media del planeta al Sol. Por las propiedades de la elipse, se cumple que su valor coincide con el semieje mayor de la elipse (a)
El valor de la constante de proporcionalidad k se puede calcular mediante la siguiente ecuación:
Donde G es la constante de gravitación universal y M es la masa del planeta.
La fórmula de la tercera ley de Kepler también puede expresarse comparando el periodo orbital y el la distancia media al Sol de dos planetas diferentes, esto es, de la siguiente forma:
La tercera ley de Kepler significa que cuanto mayor es la órbita de un planeta, mayor es su período orbital y, por tanto, menor es su velocidad media.
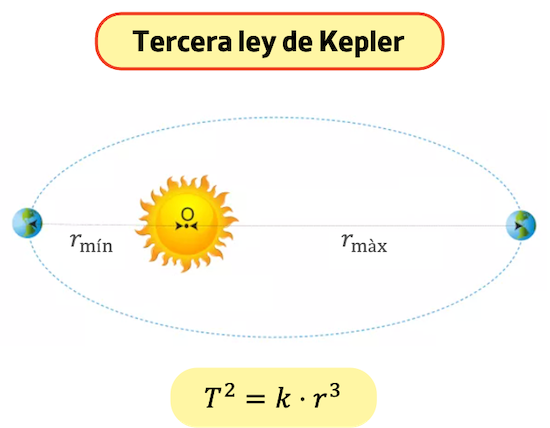
En la siguiente tabla puedes ver el periodo orbital y el radio medio de la órbita de cada planeta del Sistema Solar.
| Planeta | Periodo orbital T (años) | Radio medio (1010 m) |
|---|---|---|
| Mercurio | 0,241 | 5,79 |
| Venus | 0,615 | 10,8 |
| Tierra | 1 | 15,0 |
| Marte | 1,88 | 22,8 |
| Júpiter | 11,9 | 77,8 |
| Saturno | 29,5 | 143 |
| Urano | 84 | 287 |
| Neptuno | 165 | 450 |
