▷ Plano inclinado (física): fórmulas y ejercicios resueltos

En este artículo se explica qué son los planos inclinados en física y cómo se resuelven los problemas de este tipo. Así que encontrarás las fórmulas de las fuerzas que actúan en un plano inclinado y, además, podrás practicar con ejercicios resueltos paso a paso del plano inclinado.

Índice

¿Qué es un plano inclinado?

Un plano inclinado es una superficie inclinada un determinado ángulo. En física, se usa el plano inclinado para practicar problemas de fuerzas.

Por ejemplo, una rampa o un camino con pendiente son planos inclinados.

El plano inclinado sirve para transportar un objeto haciendo menos fuerza. Ya que empujar un objeto por un plano inclinado requiere de menos fuerza que levantarlo verticalmente.

Además, el plano inclinado es considerado como una de las seis máquinas simples clásicas.

Fórmulas del plano inclinado

Ahora que ya sabemos la definición de plano inclinado, vamos a ver cuáles son las fórmulas que actúan en un plano inclinado y cuáles son las ecuaciones que nos permiten relacionarlas.

El primer problema que nos encontramos en los ejercicios de planos inclinados, es que la mayoría de fuerzas actúan en dirección paralela o perpendicular al plano inclinado. De modo que los ejes de coordenadas típicos (un eje vertical y un eje horizontal) no resultan muy útiles para este tipo de problemas. Es por eso que, en general, en los planos inclinados se trabaja con un sistema de coordenadas diferente:

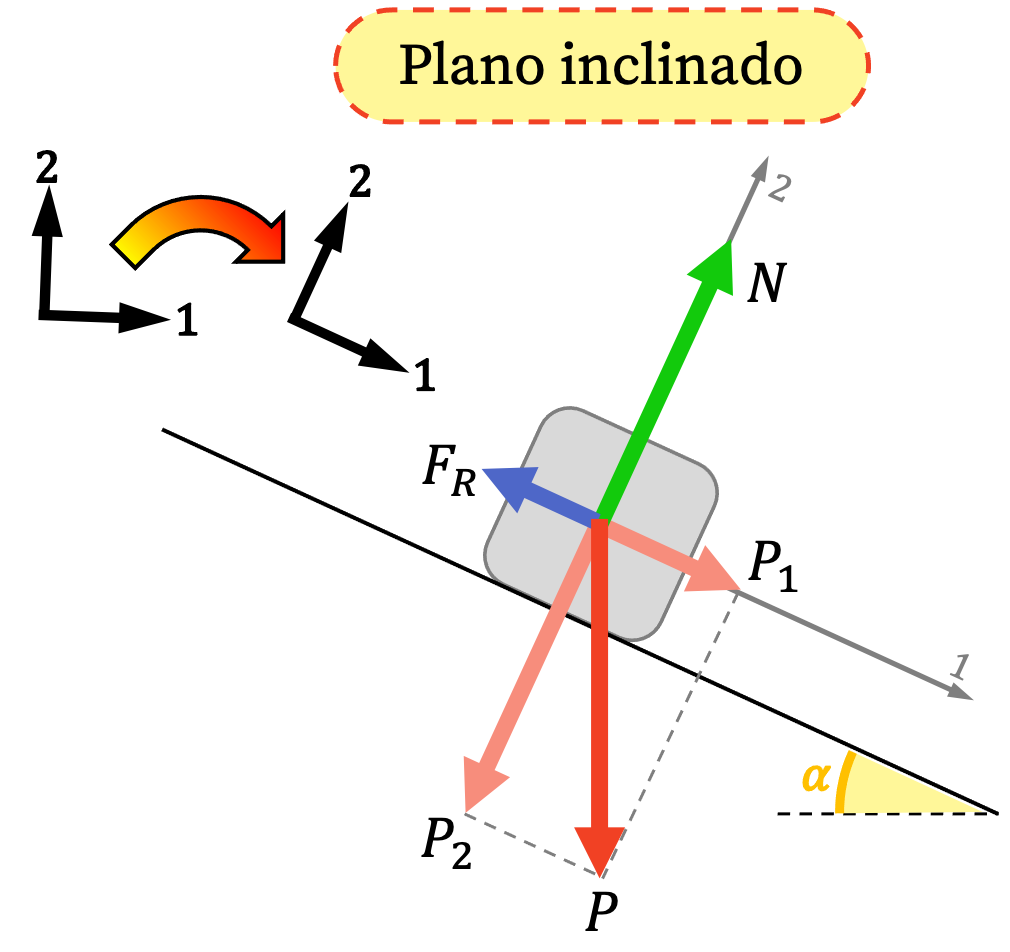
En física, para resolver un problema del plano inclinado se usan dos ejes diferentes: un primer eje cuya dirección es paralela al plano inclinado y, por otro lado, un segundo eje cuya dirección es perpendicular al plano inclinado.

Además, tal y como puedes ver en la imagen, en un plano inclinado actúan generalmente tres fuerzas distintas (si hay rozamiento): la fuerza del peso, la fuerza normal y la fuerza de rozamiento (o fuerza de fricción). Aunque, lógicamente, si en el plano inclinado no hay rozamiento se desprecia la fuerza de rozamiento.

Sin embargo, la fuerza del peso se descompone vectorialmente en dos componentes: una componente paralela al plano inclinado y otra componente perpendicular al plano inclinado. De esta forma todas las fuerzas se pueden expresar en los ejes de trabajo del plano inclinado. Así pues, las dos componentes del peso del cuerpo apoyado sobre el plano inclinado se calculan mediante el seno y el coseno del ángulo de inclinación:

$P_1=m\cdot g\cdot \text{sen}(\alpha)$

$P_2=m\cdot g\cdot \text{cos}(\alpha)$

Finalmente, las fuerzas que actúan en un plano inclinado se pueden relacionar mediante las siguientes dos fórmulas:

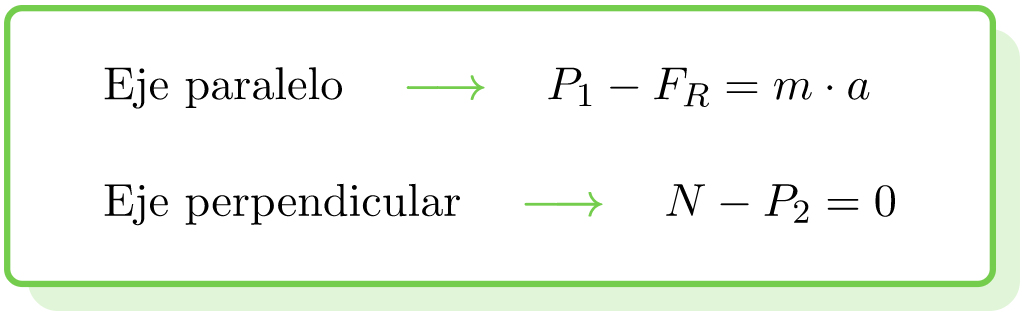
Fíjate que, si el enunciado del problema no dice lo contrario, el cuerpo situado en el plano inclinado se podría deslizar por la pendiente, por eso en la ecuación del eje paralelo al plano se incluye una posible aceleración. En cambio, el cuerpo no se puede mover en la dirección del eje perpendicular al plano inclinado, así que el sumatorio de fuerzas da como resultado cero.

Ejemplo resuelto del plano inclinado

Para que puedas ver cómo se resuelven los problemas de planos inclinados en física, a continuación puedes ver un ejemplo resuelto paso a paso.

Colocamos un cuerpo de masa m=6 kg encima de un plano inclinado 45º. Si el cuerpo se desliza por el plano inclinado con una aceleración de 4 m/s², ¿cuál es el coeficiente de fricción dinámico entre la superficie del plano inclinado y la del cuerpo? Datos: g=10 m/s².

problema del coeficiente de friccion o de rozamiento dinamico

Lo primero que debemos hacer para resolver cualquier problema de física sobre dinámica es dibujar el diagrama de cuerpo libre. Así pues, todas las fuerzas que actúan en el sistema son las siguientes:

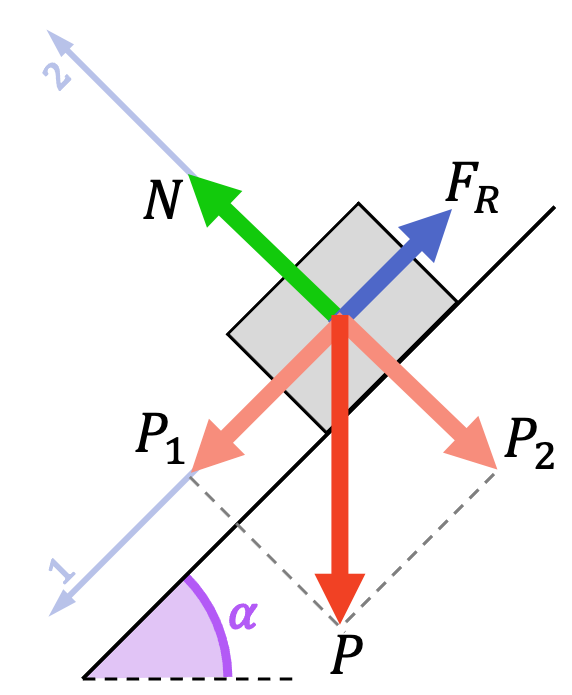
ejercicio resuelto del coeficiente de fricción o de rozamiento dinámico

En la dirección del eje 1 (paralelo al plano inclinado) el cuerpo tiene una aceleración, en cambio, en la dirección del eje 2 (perpendicular al plano inclinado) el cuerpo está en reposo. A partir de esta información, planteamos las ecuaciones de las fuerzas del sistema:

$P_1-F_R=m\cdot a$

$P_2-N=0$

Así pues, podemos calcular la fuerza normal de la segunda ecuación:

$\begin{array}{l}N=P_2\\[3ex]N=m\cdot g\cdot \text{cos}(\alpha) \\[3ex] N=6 \cdot 10 \cdot \text{cos}(45º)\\[3ex]N=42,43 \ N\end{array}$

Por otro lado, calculamos el valor de la fuerza de rozamiento (o fuerza de fricción) de la primera ecuación planteada:

$\begin{array}{l}P_1-F_R=m\cdot a\\[3ex]F_R=P_1-m\cdot a\\[3ex]F_R=m\cdot g\cdot \text{sen}(\alpha)-m\cdot a\\[3ex]F_R=6\cdot 10\cdot \text{sen}(45º)-6\cdot 4\\[3ex]F_R=18,43 \ N\end{array}$

Y una vez ya conocemos el valor de la fuerza normal y de la fuerza de rozamiento, podemos determinar el coeficiente de fricción dinámico utilizando su fórmula correspondiente:

$\mu_d=\cfrac{F_R}{N}=\cfrac{18,43}{43,43}=0,42$

Ejercicios resueltos del plano inclinado

Ejercicio 1

Colocamos un cuerpo de masa m=2 kg encima de un plano inclinado con un ángulo de inclinación de 30º. ¿Cuál es el coeficiente de fricción entre la rampa y el cuerpo si se mantiene en equilibrio? Datos: g=9,81 m/s²

Ver solución

Como en cualquier problema de física sobre fuerzas, lo primero que debemos hacer es dibujar el diagrama de cuerpo libre del sistema. Así pues, todas las fuerzas que actúan en este sistema son:

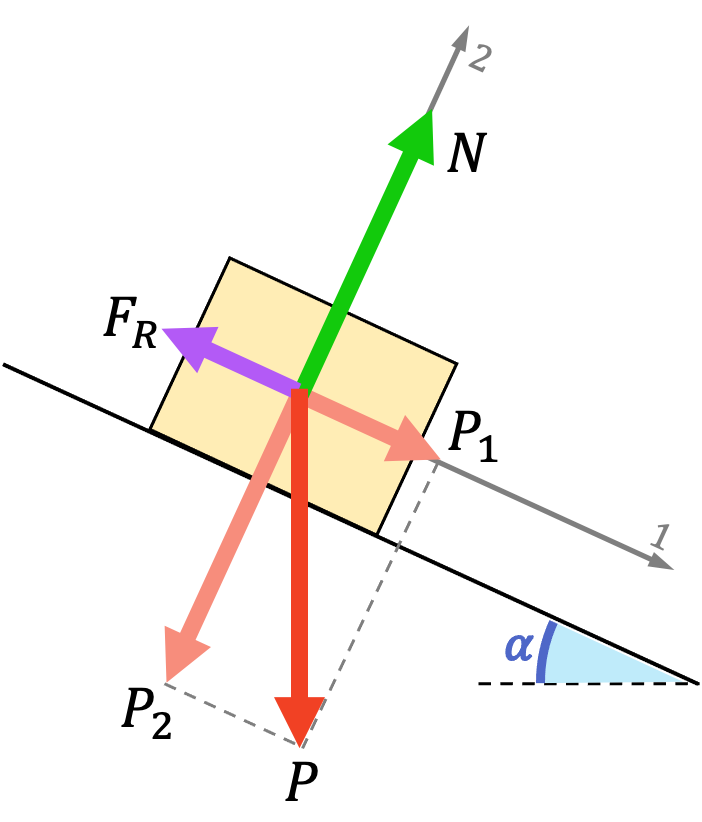
ejercicio resuelto de la fuerza normal y fuerza de rozamiento

Entonces, para que el sistema esté en equilibrio, el sumatorio de fuerzas en los ejes 1 y 2 deben ser iguales a cero. Por lo tanto, se cumplen la siguientes ecuaciones:

$F_R=P_1$

$N=P_2$

Ahora podemos calcular el valor de la fuerza normal a partir de la segunda ecuación:

$\begin{array}{l}N=P_2\\[3ex]N=P\cdot \text{cos}(\alpha)\\[3ex]N=m \cdot g\cdot \text{cos}(\alpha)\\[3ex]N=2 \cdot 9,81 \cdot \text{cos}(30\text{º})\\[3ex]N=16,99 \ N\end{array}$

Por otro lado, determinamos el valor de la fuerza de rozamiento utilizando la primera ecuación:

$\begin{array}{l}F_R=P_1\\[3ex]N=P\cdot \text{sen}(\alpha)\\[3ex]F_R=m \cdot g\cdot \text{sen}(\alpha)\\[3ex]F_R=2 \cdot 9,81 \cdot \text{sen}(30\text{º})\\[3ex]F_R=9,81 \ N\end{array}$

Asimismo, la fuerza de rozamiento se puede relacionar con la fuerza normal y el coeficiente de fricción mediante la siguiente fórmula:

$F_R=\mu \cdot N$

De modo que despejamos el coeficiente de fricción de la ecuación y calculamos su valor:

$\mu=\cfrac{F_R}{N}$

$\mu=\cfrac{9,81}{16,99}$

$\bm{\mu=0,58}$

Ejercicio 2

Tal y como se ve en el siguiente sistema formado por un plano inclinado y una polea, dos cuerpos están conectados por una cuerda y una polea de masas despreciables. Si el cuerpo 2 tiene una masa m₂=7 kg y la inclinación de la rampa es de 50º, calcula la fuerza normal que ejerce el plano inclinado sobre el cuerpo de masa m₁ para que todo el sistema esté en equilibrio. Desprecia la fuerza de rozamiento en todo el ejercicio.

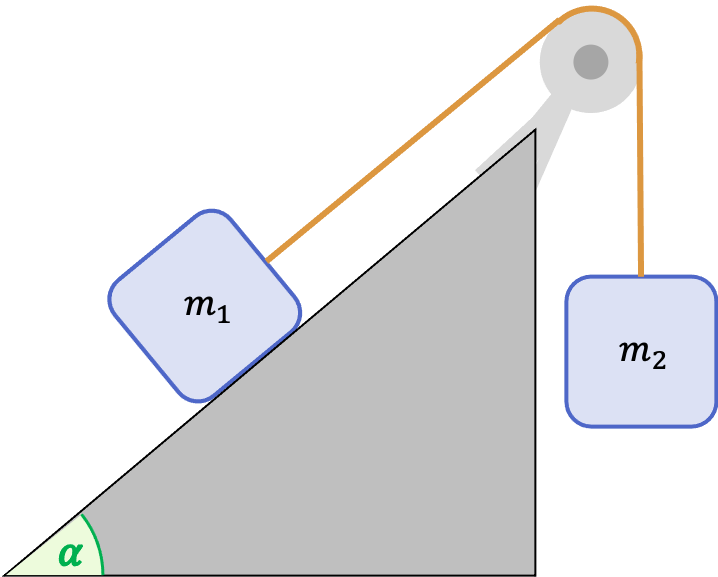
problema sobre el equilibrio traslacional

Ver solución

El cuerpo 1 está sobre una pendiente inclinada, por lo tanto, lo primero que debemos hacer es descomponer vectorialmente la fuerza de su peso para tener las fuerzas en los ejes de la pendiente:

$P_{1x}=P_1\cdot \text{sen}(\alpha)$

$P_{1y}=P_1\cdot \text{cos}(\alpha)$

De modo que el conjunto de fuerzas que actúan en todo el sistema son:

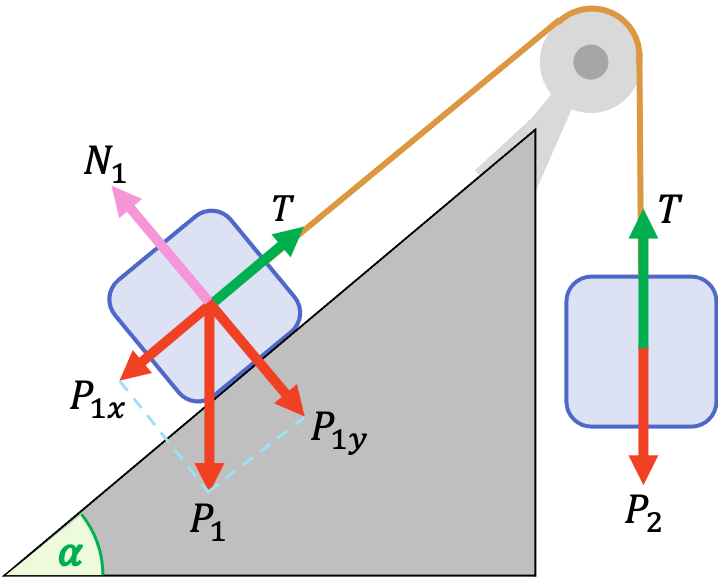
ejercicio resuelto de equilibrio traslacional

El enunciado del problema nos dice que el sistema de fuerzas está en equilibrio, por lo que los dos cuerpos deben estar en equilibrio. A partir de esta información podemos plantear las ecuaciones de equilibrio de los dos cuerpos:

$1\ \rightarrow \ \begin{cases}P_{1x}=T\\[2ex]P_{1y}=N\end{cases} \qquad\qquad 2 \ \rightarrow \ T=P_2$

Por lo tanto, la componente vectorial del peso del cuerpo 1 inclinada en el sentido de la pendiente debe ser igual al peso del objeto 2.

$P_{1x}=P_2$

$P_1\cdot \text{sen}(\alpha)=P_2$

De la ecuación anterior podemos calcular la masa del cuerpo 1:

$m_1\cdot g \cdot \text{sen}(\alpha) =m_2 \cdot g$

$m_1 \cdot \text{sen}(\alpha) =m_2$

$m_1 \cdot \text{sen}(50\text{º}) =7$

$m_1 =\cfrac{7}{\text{sen}(50\text{º})}$

$m_1=9,14 \ kg$

Por otro lado, si nos fijamos en el diagrama de fuerzas del sistema, observamos que la fuerza normal debe ser igual a la componente vectorial del peso del cuerpo 1 perpendicular al plano inclinado.

$P_{1y}=N$

$P_1\cdot \text{cos}(\alpha)=N$

Así pues, de esta ecuación podemos hallar el valor de la fuerza normal:

$\begin{array}{l}N=P_1\cdot \text{cos}(\alpha)\\[3ex]N=m_1 \cdot g\cdot \text{cos}(\alpha)\\[3ex]N=9,14 \cdot 9,81 \cdot \text{cos}(50\text{º})\\[3ex]N=\bm{57,63 \ N}\end{array}$

Ejercicio 3

Un trineo de 70 kg se desliza por una pendiente de 30º de inclinación con una velocidad inicial de 2 m/s. Si el coeficiente de rozamiento dinámico entre el trineo y la nieve es de 0,2, calcula la velocidad que adquirirá el trineo después de recorrer 20 metros. Datos: g=10 m/s².

Ver solución

Primero de todo, hacemos el diagrama de cuerpo libre de el trineo:

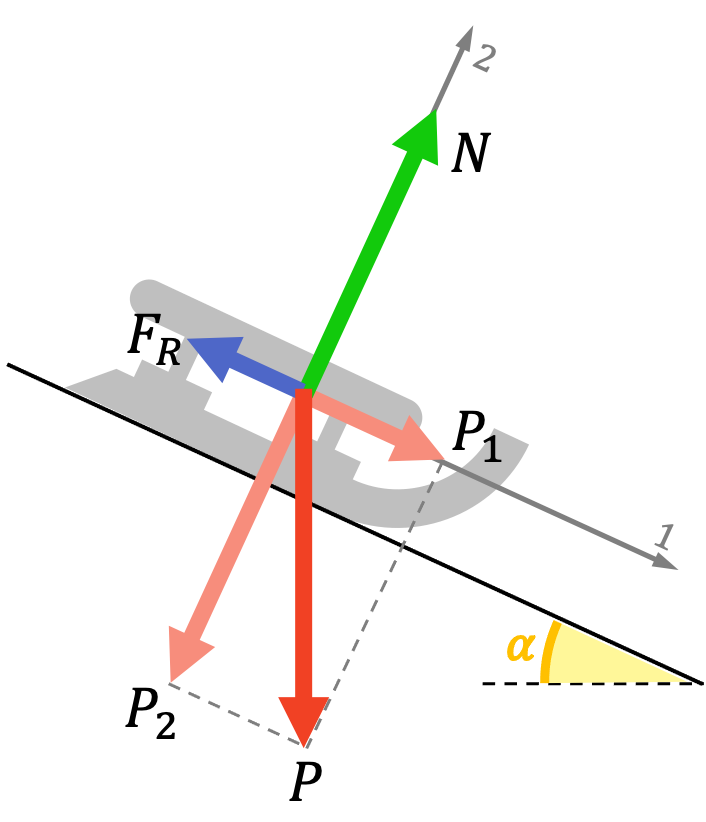
ejercicio resuelto de la fuerza de rozamiento o fricción en un plano inclinado

El trineo tiene aceleración en la dirección del eje 1 (paralelo al plano inclinado) pero se mantiene en reposo en la dirección del eje 2 (perpendicular al plano inclinado), por lo tanto, las ecuaciones de las fuerzas son:

$P_1-F_R=m\cdot a$

$P_2-N=0$

A partir de la segunda ecuación, podemos calcular la fuerza normal que actúa sobre el trineo

$\begin{array}{l}N=P_2\\[3ex]N=m\cdot g\cdot \text{cos}(\alpha) \\[3ex] N=70 \cdot 10 \cdot \text{cos}(30º)\\[3ex]N=606,22 \ N\end{array}$

Como ahora ya conocemos el valor de la fuerza normal y el coeficiente de fricción dinámico, podemos calcular la fuerza de fricción aplicando su fórmula correspondiente:

$F_R=\mu\cdot N=0,2 \cdot 606,22=121,24 \ N$

Así pues, para determinar la velocidad final, primero tenemos que encontrar la aceleración del trineo, y esta se pude calcular a partir de la primera ecuación de fuerzas planteada:

$P_1-F_R=m\cdot a$

$a=\cfrac{P_1-F_R}{m}$

$a=\cfrac{m\cdot g\cdot \text{sen}(\alpha)-F_R}{m}$

$a=\cfrac{70\cdot 10\cdot \text{sen}(30º)-121,24}{70}$

$a=3,27 \ \cfrac{m}{s^2}$

Una vez sabemos la aceleración del trineo, calculamos el tiempo que tarda en recorrer los 20 metros con la ecuación del movimiento rectilíneo de aceleración constante:

$x=v_0\cdot t +\cfrac{1}{2}\cdot a \cdot t^2$

$20=2\cdot t +\cfrac{1}{2}\cdot 3,27 \cdot t^2$

$0=1,64t^2+2t-20$

$\displaystyle t=\cfrac{-2\pm \sqrt{2^2-4\cdot 1,64\cdot (-20)}}{2\cdot 1,64}=\cfrac{-2\pm 11,63}{3,28}=\begin{cases}2,94\\[2ex]-4,15 \ \color{red}\bm{\times}\end{cases}$

Lógicamente, descartamos la solución negativa ya que el tiempo es una magnitud física que no puede ser negativa.

Por último, calculamos la velocidad final mediante la fórmula de la aceleración constante:

$a=\cfrac{v_f-v_0}{t_f-t_0}\quad \longrightarrow \quad v_f=a\cdot (t_f-t_0)+v_0$

$v_f=3,27\cdot (2,94-0)+2=\bm{11,61} \ \cfrac{\bm{m}}{\bm{s}}$

¿Qué es un plano inclinado?

Fórmulas del plano inclinado

Ejemplo resuelto del plano inclinado

Ejercicios resueltos del plano inclinado

Ejercicio 1

Ejercicio 2

Ejercicio 3

Deja un comentario Cancelar respuesta