Primera ley de Newton (ley de inercia)

En este artículo se explica qué dice la primera ley de Newton, también conocida como ley de inercia. Además del enunciado de la primera ley de Newton, podrás ver ejemplos de esta ley y su fórmula matemática. Por último, podrás practicar con ejercicios resueltos paso a paso de la primera ley de Newton.

¿Cuál es la primera ley de Newton?

El enunciado de la primera ley de Newton, también llamada ley de inercia, establece lo siguiente:

Por ejemplo, un objeto que está en reposo sobre el suelo no se moverá hasta que no actúe una fuerza sobre él.

Por lo tanto, la primera ley de Newton implica que si un cuerpo se desplaza en movimiento rectilíneo uniforme significa que ninguna fuerza externa actúa sobre él o que la fuerza resultante de todo el sistema es nula.

En total hay tres leyes de Newton, la que acabamos de ver que también se llama principio de inercia, la segunda ley o principio fundamental de la dinámica, y la tercera ley o principio de acción y reacción.

Lógicamente, las tres leyes reciben el nombre del físico Isaac Newton porque fue el primero que las expuso en su obra Principios matemáticos de la filosofía natural. Esta publicación es considerada como uno de los pilares de la física.

Ejemplos de la primera ley de Newton

Vista la definición de la primera ley de Newton (o ley de inercia), a continuación vamos a analizar varios ejemplos de esta regla.

1. Un claro ejemplo de primera ley de Newton es un sofá colocado en reposo sobre el suelo. Si no se ejerce ninguna fuerza sober el sofá, este no se moverá y se quedará quieto. Pero si se empuja el sofá con una fuerza suficientemente grande, el sofá adquirirá velocidad y por tanto cambiará su estado de movimiento.
2. Otro ejemplo de la primera ley de Newton es una sonda espacial moviéndose a velocidad constante por el espacio. Una vez superada la influencia gravitatoria de los planetas, en el espacio no hay rozamiento ni ninguna otra fuerza. Por lo tanto, una sonda espacial se mueve a velocidad constante por el espacio porque no actúa ninguna fuerza sobre ella.
3. Un coche desplazándose a velocidad constante también es un ejemplo de la primera ley de Newton (o ley de inercia), ya que para moverse sin aceleración la fuerza resultante debe ser nula. Cuando el coche avanza una fuerza de rozamiento actúa sobre él en contra del movimiento, así que para moverse a velocidad constante el motor del coche debe hacer una fuerza de la misma magnitud y dirección pero sentido contrario. De este modo las dos fuerzas se contrarrestan y el coche se mueve con la misma velocidad.

Fórmula de la primera ley de Newton

Para profundizar más en el concepto de la primera ley de Newton, en este apartado veremos la fórmula con la que se puede expresar dicha ley.

Matemáticamente, la fórmula de la primera ley de Newton establece que si el sumatorio de fuerzas de un sistema es igual a cero, la aceleración de dicho sistema también es nula. El recíproco también es cierto.

Asimismo, si la suma de fuerzas es nula, implica que la cantidad de movimiento (o momento lineal) es constante.

De todos modos, estas expresiones sirven solo para expresar la ley mediante álgebra. Lo importante es que entiendas el significado de la primera ley de Newton y que el sumatorio de todas las fuerzas debe ser nulo para que se cumpla.

Ejercicios resueltos de la primera ley de Newton

Ejercicio 1

¿Cuál es la fuerza que debe hacer un ascensor para subir un objeto de 7 kg?

Lo primero que debemos hacer para solucionar este problema es calcular la fuerza de la gravedad que ejerce la Tierra sobre el objeto. Para ello, usamos la fórmula de la fuerza del peso:

Entonces, según la primera ley de Newton, si el ascensor hace una fuerza vertical hacia arriba de 68,67 N el objeto se quedará quieto ya que la fuerza resultante será nula. Así que el ascensor debe hacer una fuerza superior a 68,67 N para que empiece a subir.

 

Ejercicio 2

Un ascensor está subiendo un cuerpo cuya masa es de 100 kg. En un momento determinado, la fuerza de rozamiento que se opone al movimiento es de 300 N y la fuerza que ejerce el cable hacia arriba es de 1100 N. ¿El ascensor está acelerando, frenando, o moviéndose a velocidad constante?

En primer lugar, calculamos la fuerza gravitatoria que hace la Tierra sobre el cuerpo con la fórmula del peso:

De modo que la suma total del conjunto de fuerzas que tiran el ascensor hacia abajo es:

Por otro lado, la única fuerza que empuja el ascensor hacia arriba es la del cable.

De manera que la suma de fuerzas hacia abajo es mayor que las fuerzas hacia arriba, por lo tanto, el ascensor se está frenando en este momento.

 

Ejercicio 3

Una caja con masa de 60 kg es arrastrada por una cuerda que forma un ángulo de 30º con el suelo. Si se necesita hacer una fuerza de 120 N sobre la cuerda para mover la caja con una velocidad constante de 10 m/s, ¿cuál es el valor aproximado del coeficiente de rozamiento cinético entre la caja y el suelo?

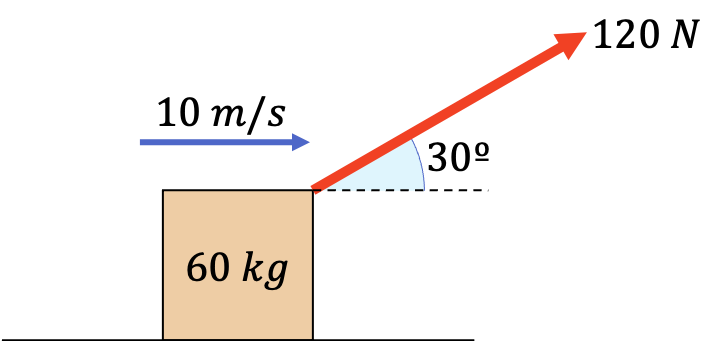
Como sabemos el ángulo de inclinación de la fuerza aplicada, podemos descomponerla en una fuerza vertical y una fuerza horizontal aprovechando las razones trigonométricas:

Por otro lado, calculamos la fuerza del peso que ejerce la Tierra sobre la caja:

De modo que el diagrama de cuerpo libre del sistema es:

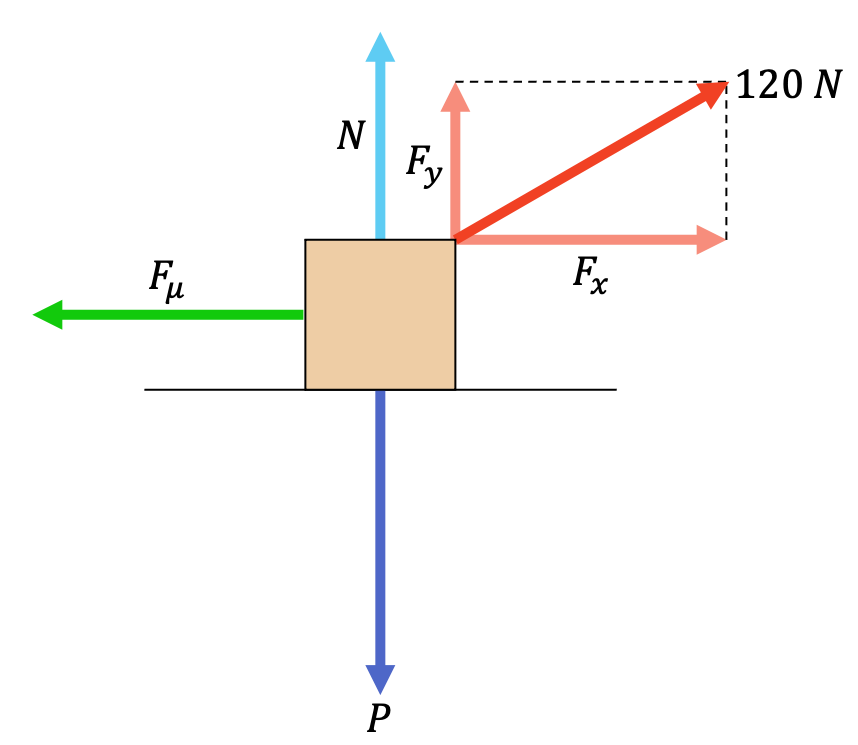
Ten en cuenta que las fuerzas F_x y F_y representadas son solo la descomposición de la fuerza de 120 N, por lo que no actúan a la vez sino que las dos fuerzas sustituyen a la fuerza de 120 N.

Como la caja se mueve a velocidad constante implica que está en equilibrio, por lo que podemos aplicar las condiciones de equilibrio para resolver el ejercicio. Primero planteamos la ecuación de equilibrio vertical para hallar la fuerza normal:

Y finalmente planteamos la ecuación de equilibrio horizontal para determinar el coeficiente de rozamiento: