En este post se explica qué son las cuñas (máquinas simples). Así pues, encontrarás en qué consiste una cuña cuando es una máquina simple, su fórmula y sus aplicaciones. Además, podrás practicar con un problema resuelto paso a paso.
Índice
¿Qué es una cuña (máquina simple)?
Una cuña es una pieza en forma de triángulo que es normalmente de madera o de metal y termina con un ángulo muy agudo. La cuña es considerada una de las seis máquinas simples.
Como máquina simple, se usa la forma de la cuña para cambiar la dirección de la fuerza que se le aplica. Así pues, la cuña sirve para separar un objeto en dos, levantar un objeto o mantener un objeto estático en su lugar.
El funcionamiento de una cuña consiste en transformar una fuerza que se le aplica a su extremo en dos fuerzas perpendiculares a sus superficies inclinadas. Por lo tanto, una cuña es una máquina simple que permite cambiar la dirección de una fuerza.

En un primer momento, la fuerza que se ejerce sobre la superficie plana de la cuña se transfiere a su extremo puntiagudo, lo que permite penetrar en un objeto. Luego, al introducir la cuña en el agujero creado, la fuerza que se aplica en su superficie plana se convierte en dos fuerzas de dirección perpendicular a las caras inclinadas de la cuña, separando así el objeto en dos partes.
Fórmula de la cuña como máquina simple
La ventaja mecánica de una cuña es la relación entre su altura y su ancho. Por lo tanto, la ventaja mecánica de una cuña como máquina simple es igual a la longitud de su altura partido por su ancho.
De modo que la fórmula de la máquina simple de la cuña es la siguiente:
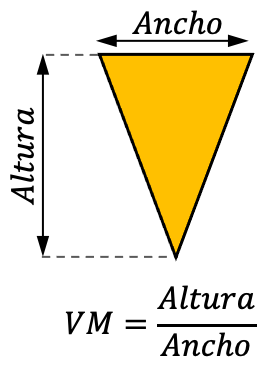
Así pues, la ventaja mecánica es directamente proporcional a la altura de la cuña y, por otro lado, es inversamente proporcional al ancho de la cuña. Por lo tanto, el ángulo de la cuña determina la ventaja mecánica de este tipo de máquina simple.
En definitiva, cuanto menor sea el ángulo entre las cara inclinadas, más ventaja mecánica tendrá la máquina simple de la cuña. Lo que significa que menos fuerza se deberá hacer para vencer a la resistencia.
Uso de la cuña
Una vez hemos visto cuál es la definición de cuña como máquina simple y cuál es su fórmula, vamos a ver los usos de la cuña para acabar de entender su significado.
Ejemplos muy claros del uso de la cuña para romper o dividir un cuerpo son el hacha y el clavo, que pueden penetrar un objeto y posteriormente separarlo en dos mediante el mecanismo de la máquina simple de la cuña. Por ejemplo, la madera se puede cortar utilizando un hacha.
Asimismo, el cuchillo, las tijeras y los cinceles también se basan en el funcionamiento de la cuña como máquina simple para dividir un objeto en dos.
Por otro lado, otra aplicación de la falca es la de inmovilizar un objeto. Por ejemplo, se puede poner una cuña en el pie de una puerta para aguantarla y que no se mueva, de este modo se impide que se cierre la puerta por una corriente de aire.
Ejercicio resuelto de la cuña
Se aplica un fuerza vertical de valor F=10 N sobre la siguiente cuña cuyo ángulo mide 40º. ¿Cuál es la fuerza R que ejerce cada una de sus caras inclinadas?

En primer lugar, hacemos el diagrama de cuerpo libre de la cuña. Así que representamos todas las fuerzas que actúan en el sistema:

Ten en cuenta que Rx y Ry son las fuerzas que se obtienen al descomponer vectorialmente la fuerza que hace cada una de las caras inclinadas de la cuña (R), y se calculan mediante las siguientes fórmulas:
Por lo tanto, si planteamos la ecuación vertical de las fuerzas que actúan en el sistema obtenemos la siguiente expresión:
Ahora sustituimos la expresión de la fuerza Ry en la ecuación:
Y, finalmente, sustituimos los datos en la ecuación y despejamos la incógnita:
