En este artículo te explicamos en qué consiste la ley de Biot-Savart. Así pues, encontrarás qué dice la ley de Biot-Savart, cuál es la fórmula de la ley de Biot-Savart y cuáles son sus aplicaciones.
Índice
¿Qué es la ley de Biot-Savart?
La ley de Biot-Savart es una ley del electromagnetismo que permite calcular el campo magnético que genera una corriente eléctrica.
En concreto, la ley de Biot-Savart relaciona el campo magnético con la magnitud, la dirección, la longitud y la distancia a la corriente eléctrica.
La ley de Biot-Savart recibe este nombre en honor a los físicos franceses Jean-Baptiste Biot y Félix Savart, quien descubrieron esta ecuación en 1820 después de que Oersted demostrará que las corrientes eléctricas generan campos magnéticos.
Fórmula de la ley de Biot-Savart
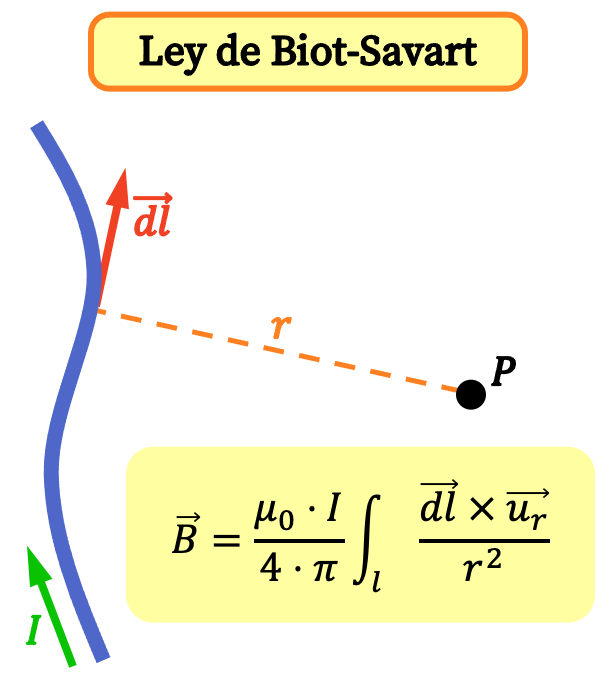
La ley de Biot-Savart dice que el campo magnético generado por una corriente eléctrica estacionaria en un punto se puede calcular con la siguiente fórmula:
Donde:
es el valor del campo magnético, expresado en teslas (T).
es la permeabilidad magnética en el vacío, cuyo valor es de 4π·10−7 N/A2.
es la intensidad de la corriente eléctrica, expresada en amperios (A).
es el elemento infinitesimal de longitud del circuito.
es la distancia desde el conductor hasta el punto en el que se calcula el campo magnético, expresado en metros (m).
es el vector unitario de
.
Con la fórmula anterior se puede determinar el vector del campo magnético, pero también se puede hallar directamente su intensidad con la siguiente expresión:
Donde es el ángulo que forman
y
.
Fórmula del campo magnético creado por un conductor rectilíneo
La intensidad del campo magnético generado por un conductor de electricidad recto es igual a la permeabilidad magnética multiplicado por la intensidad de la corriente eléctrica dividido por dos por pi y por la distancia al conductor.
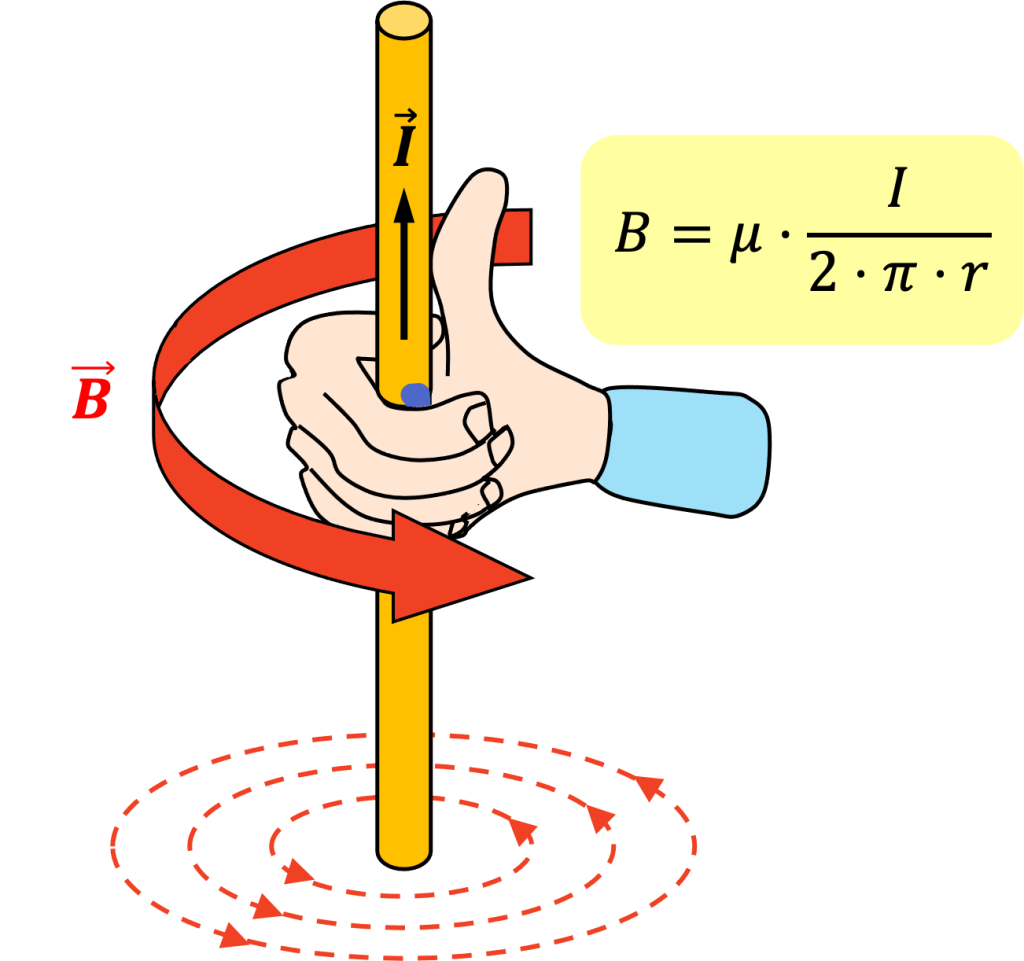
Por lo tanto, la fórmula de la intensidad del campo magnético creado por un conductor recto es la siguiente:
Donde:
es la intensidad del campo magnético, cuya unidad en el Sistema Internacional es el tesla (T).
es la permeabilidad magnética, cuyo valor en el vacío es 4π·10−7 N/A2.
es la intensidad de la corriente eléctrica.
es la distancia desde el conductor hasta el punto en el que se evalúa el campo magnético.
Para determinar la dirección y el sentido del campo magnético se puede utilizar la regla de la mano derecha. Este regla consiste en colocar el pulgar de la mano derecha de manera que apunte a la misma dirección que la corriente eléctrica. Entonces, el resto de dedos de la mano derecha te indicarán el sentido del campo magnético.
Aplicaciones de la ley de Biot-Savart
La ley de Biot-Savart tiene una amplia gama de aplicaciones en física e ingeniería, como por ejemplo:
- Diseño de bobinas y solenoides: la ley de Biot-Savart es fundamental en el diseño y análisis de bobinas y solenoides, ya que permite calcular el campo magnético generado por una corriente eléctrica que fluye a través de estas estructuras, lo que es esencial en la construcción de transformadores, motores eléctricos, actuadores electromagnéticos y otros dispositivos electromecánicos.
- Magnetostática: la ley de Biot-Savart se utiliza para calcular el campo magnético en situaciones estáticas, es decir, cuando no hay cambios en el tiempo. Esto es útil en la caracterización de imanes permanentes y en el diseño de sistemas magnéticos estáticos, como sistemas de levitación magnética y dispositivos de separación magnética.
- Electrodinámica: en situaciones donde las corrientes eléctricas cambian con el tiempo, la ley de Biot-Savart se combina con la ley de Ampère para determinar el campo magnético. Esta combinación es fundamental en el análisis de circuitos eléctricos, antenas, dispositivos de radiofrecuencia y otras aplicaciones donde las corrientes alternas son importantes.
