▷ Energía potencial eléctrica

En este artículo te explicamos qué es la energía potencial eléctrica. También encontrarás cómo calcular la energía potencial eléctrica junto con un ejemplo resuelto. Además, podrás ver cuál es la relación entre la energía potencial eléctrica y otras magnitudes eléctricas.

Índice

¿Qué es la energía potencial eléctrica?

La energía potencial eléctrica (o energía potencial electrostática) es la energía que adquiere una carga eléctrica debido a su posición en un campo eléctrico. Es decir, la energía potencial eléctrica es aquella energía que ganan las cargas eléctricas por su posición en relación con otras cargas.

Por lo tanto, la energía potencial eléctrica resulta de la fuerza eléctrica. Cuando se juntan dos o más cuerpos cargados eléctricamente, aparecen fuerzas eléctricas entre ellos que los atraen o los repelen. En consecuencia, los cuerpos ganan o pierden energía potencial eléctrica.

Por ejemplo, si dos cargas eléctricas q_A y q_B están más próximas entre sí que las cargas q_C y q_D y todas las cargas tienen el mismo valor, la energía potencial eléctrica de las cargas q_A y q_B será mayor porque al estar más cerca interaccionan de manera más fuerte y por tanto la fuerza eléctrica es mayor.

Es importante no confundir la energía potencial eléctrica con el potencial eléctrico, pues son dos conceptos diferentes. Más abajo veremos cuál es la diferencia y cuál es la relación entre ellos.

Ten en cuenta que a veces se distingue entre la energía potencial eléctrica y la energía potencial electrostática. Así pues, el término «energía potencial eléctrica» se refiere a la energía potencial de un sistema con campos eléctricos que varían en el tiempo, mientras que el término «energía potencial electrostática» se refiere a la energía potencial en sistemas con campos eléctricos constantes.

Fórmula de la energía potencial eléctrica

La energía potencial eléctrica de una carga en un punto se define como el trabajo realizado por una fuerza externa para desplazar dicha carga desde el infinito hasta dicho punto.

$E_{p_A}=W_{f(\infty\to A)}$

Entonces, como el trabajo realizado por una fuerza externa equivale al trabajo eléctrico cambiado de signo, la energía potencial de una carga en un punto es el opuesto del trabajo realizado por la fuerza eléctrica para desplazar dicha carga desde el infinito hasta dicho punto.

$E_{p_A}=W_{f(\infty\to A)}=-W_{e(\infty\to A)}$

Por lo tanto, la variación de energía potencial eléctrica por una carga al desplazarse desde un punto A hasta otro punto B es equivalente al trabajo eléctrico realizado debido al desplazamiento entre esos dos puntos cambiado de signo.

$\Delta E_{p_{AB}}=E_{p_B}-E_{p_A}=-W_{e(A \to B)}$

➤ Ver: Trabajo eléctrico

Energía potencial eléctrica de dos cargas puntuales

La energía potencial eléctrica de un sistema de dos cargas puntuales es igual a la constante de Coulomb por la los valores de las cargas eléctricas dividido por la distancia que las separa.

Por lo tanto, la fórmula de la energía potencial eléctrica de dos cargas puntuales es E_p=K·Q·q/r.

Ver demostración de la fórmula

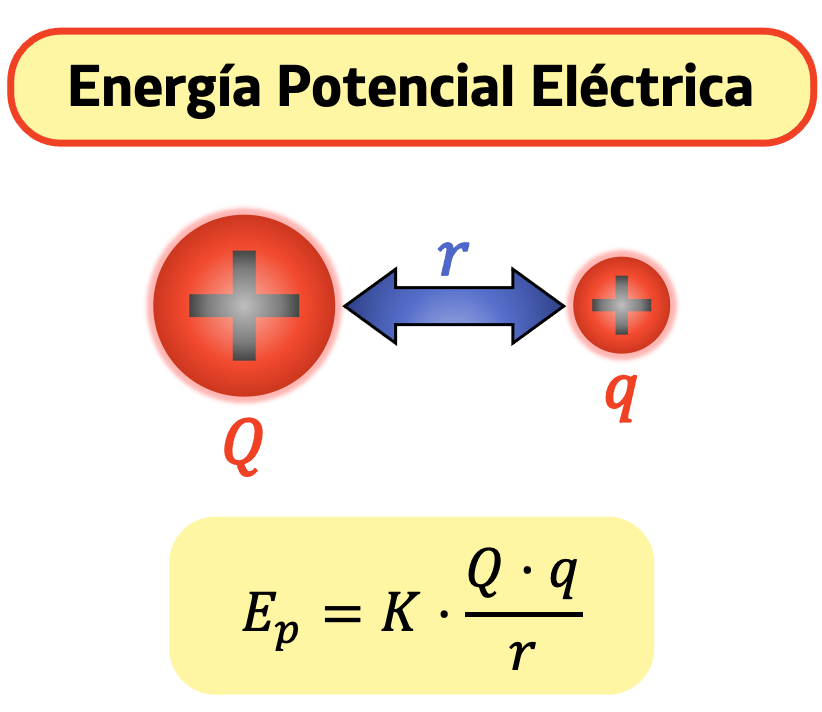
Si el sistema está formado por dos cargas puntuales q y Q, la energía potencial eléctrica es equivalente al trabajo que se debe hacer para desplazar la carga q hasta un punto A próximo a Q desde el infinito hasta dicho punto.

$E_{p_A}=W_{f(\infty\to A)$

Y el trabajo realizado por una fuerza externa equivale al opuesto del trabajo eléctrico

$E_{p_A}=W_{f(\infty\to A)}=-W_{e(\infty\to A)}$

Ahora aplicamos la fórmula del trabajo eléctrico:

$\displaystyle E_{p_A}=W_{f(\infty\to A)}=-W_{e(\infty\to A)}=-\int_\infty ^A F_e\cdot dr =$

$\displaystyle = - K\cdot Q\cdot q\cdot \int _\infty ^A\frac{1}{r^2}\cdot dr= - K\cdot Q\cdot q\cdot \left[-\frac{1}{r}\right]_\infty^A=K\cdot \frac{Q\cdot q}{r}$

Y de esta forma llegamos a la fórmula de la energía potencial para un sistema de dos cargas puntuales:

$\displaystyle E_{p_A}=K\cdot \frac{Q\cdot q}{r}$

Por lo tanto, según el signo de las cargas la energía potencial eléctrica será positiva o negativa

Si las dos cargas tienen el mismo signo, la energía potencial eléctrica es positiva.
Si las dos cargas tienen diferente signo, la energía potencial eléctrica es negativa.

Energía potencial eléctrica de un sistema de más dos cargas puntuales

Acabamos de ver cómo determinar la energía potencial eléctrica de un sistema de dos cargas puntuales, que es uno de los casos más sencillos. Sin embargo, el cálculo puede complicarse si tenemos tres o más cargas en el sistema.

La energía potencial de un sistema compuesto por un conjunto de cargas puntuales equivale al trabajo necesario que debería realizar una fuerza exterior para situar todas las cargas en esas posiciones trasladándolas desde el infinito.

Por lo tanto, la energía potencial de un sistema de más de dos cargas puntuales es la suma de la energía potencial eléctrica entre cada pareja de cargas.

Por ejemplo, si tenemos tres cargas q₁, q₂, q₃ en el sistema, la energía potencial eléctrica total es igual a la energía potencial eléctrica entre q₁ y q₂ más la energía potencial eléctrica entre q₁ y q₃ más la energía potencial eléctrica entre q₂ y q₃.

$\displaystyle E_{p_T}=E_{p_{12}}+E_{p_{13}}+E_{p_{23}}$

$\displaystyle E_{p_T}=K\cdot \frac{q_1\cdot q_2}{r_{12}}+K\cdot \frac{q_1\cdot q_3}{r_{13}}+K\cdot \frac{q_2\cdot q_3}{r_{23}}$

Ejercicio resuelto de la energía potencial eléctrica

Dos cargas q₁=6 mC y q₂=2 mC se encuentran fjias en el vacío a una distancia de 60 cm. Luego movemos la carga q₂ a una distancia de 1,5 m de la carga q₁. Calcula:
1. La variación de energía potencial eléctrica de la carga q₂.
2. El trabajo realizado por la fuerza eléctrica que ejerce q₁ sobre q₂.

En este problema tenemos un sistema formado por dos cargas puntuales, así que para calcular la energía potencial eléctrica de la carga q₂ tenemos que aplicar la fórmula que hemos visto más arriba:

$\displaystyle E_{p}=K\cdot \frac{q_1\cdot q_2}{r}$

$\displaystyle E_{p_i}=9\cdot 10^9 \cdot \frac{0,006\cdot 0,002}{0,60}=180000 \ J$

$\displaystyle E_{p_f}=9\cdot 10^9 \cdot \frac{0,006\cdot 0,002}{1,5}=72000 \ J$

Entonces, la variación de la energía potencial eléctrica es la diferencia entre la energía potencial eléctrica final y la energía potencial eléctrica inicial:

$\begin{aligned}\Delta E_p&=E_{p_f}-E_{p_i}\\[2ex]\Delta E_p&=72000-180000\\[2ex]\Delta E_p&=-108000\ J \end{aligned}$

Finalmente, por definición sabemos que la variación de energía potencial eléctrica en una carga al desplazarse desde un punto A hasta otro punto B es equivalente al opuesto del trabajo eléctrico realizado para desplazar la carga entre esos dos puntos, por lo tanto:

$W_{e(A \to B)}=-\Delta E_{p_{AB}}=108000 \ J$

Energía potencial eléctrica y potencial eléctrico

Por último, vamos a ver la relación entre la energía potencial eléctrica y la diferencia de potencial eléctrico ente dos puntos.

El potencial eléctrico de una carga en un punto se puede calcular dividiendo la energía potencial eléctrica de esa carga en ese punto por el valor de la carga eléctrica.

$V=\cfrac{E_p}{q}$

Por lo tanto, la diferencia de potencial que adquiere una carga q al desplazarse en presencia de un campo eléctrico desde un punto A hasta otro punto B es la variación de energía potencial eléctrica dividido por el valor de la carga que se ha desplazado.

$\Delta V_{AB}=\cfrac{\Delta E_p}{q}$

$V_B-V_A=\cfrac{E_{p_B}-E_{p_A}}{q}$

➤ Ver: ¿Qué es el potencial eléctrico?

Energía potencial eléctrica y campo eléctrico

Solo tiene sentido hablar de energía potencial eléctrica si existe un campo eléctrico, por lo tanto, la energía potencial eléctrica y el campo eléctrico están relacionados.

En concreto, la energía potencial eléctrica se puede calcular a partir de la expresión del campo eléctrico mediante la siguiente fórmula:

$\displaystyle E_{p_A}=-q \int_\infty^A \vv{E}\cdot d\vv{r}$

Asimismo, la fórmula para hallar la variación de energía potencial eléctrica con el campo eléctrico es la siguiente:

$\displaystyle \Delta E_{p_{AB}}=E_{p_B}-E_{p_A}=-q \int_A^B \vv{E}\cdot d\vv{r}$

➤ Ver: Campo eléctrico creado por una carga puntual