▷ Inducción electromagnética

En este post se explica en qué consiste la inducción electromagnética y cuándo se produce. También encontrarás cuál es la fórmula de la inducción electromagnética junto con varios problemas resueltos para acabar de comprender el concepto.

Índice

¿Qué es la inducción electromagnética?

La inducción electromagnética, también llamada inducción magnética, es un fenómeno que consiste en que un campo magnético genera una corriente eléctrica en un cuerpo sin establecer contacto físico.

La inducción electromagnética se produce cuando varía el flujo magnético en el tiempo. Es decir, si cambia la intensidad del campo magnético, su orientación o la superficie afectada por el campo magnético, se produce el fenómeno de la inducción electromagnética. Más abajo veremos cuál es la fórmula de la inducción electromagnética.

Cuando ocurre una variación del flujo magnético, se transfiere energía electromagnética al cuerpo expuesto a dicho flujo magnético, lo que provoca una tensión inducida llamada fuerza electromotriz (f.e.m.) que causa una corriente eléctrica.

El fenómeno de la inducción electromagnética fue descubierto por Michael Faraday en 1831 mediante el conocido experimento de Faraday.

Fórmula de la inducción electromagnética

La fórmula que permite calcular la inducción electromagnética viene definida por la ley de Faraday, la cual establece que cuando varía el flujo magnético se induce una tensión (fuerza electromotriz) equivalente a la variación temporal del flujo magnético cambiado de signo.

Así pues, la fórmula de la inducción electromagnética es ε=-dΦ/dt.

$\mathcal{E}=- \cfrac{d \Phi }{dt}$

Si tenemos como inductor una bobina con N espiras, tenemos que multiplicar la fórmula anterior por el número de espiras:

$\mathcal{E}=- N\cdot \cfrac{d \Phi }{dt}$

Donde:

$\mathcal{E}$ es la tensión inducida o fuerza electromotriz (fem), expresada en voltios (V).
$\Phi$ es el flujo magnético, expresado en webers (Wb).
$\cfrac{d \Phi }{dt}$ es la tasa de variación temporal del flujo magnético.
$N$ es el número de espiras de la bobina.

A esta regla, la ley de Lenz añade que el sentido de la tensión inducida es tal que su efecto se opone a la causa que lo generó. Por eso hay un signo negativo en la fórmula, ya que indica que la tensión inducida es contraria al movimiento que la provoca.

Cabe destacar que para poder aplicar esta fórmula, debes saber cómo calcular el flujo magnético, el cual es equivalente al producto entre el campo magnético, la superficie afectada por el flujo magnético y el coseno del ángulo que forman el vector del campo magnético y el vector normal a la superficie.

$\Phi=B\cdot S \cdot \text{cos}(\theta)$

Ten en cuenta que el flujo magnético puede variar por diferentes motivos: por un cambio en la intensidad del campo magnético, por un movimiento de la fuente del campo magnético, por un giro de la superficie que atraviesa el flujo magnético, etc.

➤ Ver: Ley de Ampère

Ejercicios resueltos de la inducción electromagnética

Ejercicio 1

Una espira cuadrada de longitud 12 m se encuentra inicialmente (t=0 s) a una distancia de 6 m de una región en la que hay un campo magnético de 0,4 T. Si la espira avanza a 2 m/s, calcula la expresión de la tensión inducida en función de tiempo y su valor en el instante t=5 s.

Ver solución

Para calcular la expresión que define la tensión inducida, tenemos que aplicar la fórmula de la ley de Faraday:

$\mathcal{E}=- \cfrac{d \Phi }{dt}$

El flujo magnético es igual al producto del campo magnético por la superficie por el coseno del ángulo que forman el vector del campo con el vector normal, por tanto:

$\mathcal{E}=- \cfrac{d \bigl(B\cdot S\cdot \text{cos}(0^{\text{o}})\bigr)}{dt}$

$\mathcal{E}=- \cfrac{d \left(B\cdot S\right)}{dt}$

La superficie de la fórmula se refiere al área que está dentro de la región de campo magnético. Esta superficie depende de la posición de la espira, que se va moviendo. Así pues, si llamamos x a la longitud de espira que está dentro de la zona magnética, la superficie se puede calcular elevando x al cuadrado ya que se trata de una espira cuadrada:

$\mathcal{E}=- \cfrac{d \left(B\cdot x^2\right)}{dt}$

Ahora tenemos que sustituir la variable x por una expresión equivalente que dependa del tiempo. Para ello, primero tenemos que calcular el instante en el que la espira entra en la región de campo magnético mediante la fórmula que relaciona el tiempo con la distancia y la velocidad:

$t=\cfrac{x}{v}$

$t_0=\cfrac{6}{2}=3 \ s$

Luego, como sabemos la velocidad a la que avanza la espira, podemos sustituir la variable x por el producto entre la velocidad y el tiempo. No obstante debemos añadir un retraso de 3 s a la expresión, ya que la espira entra en la zona magnética en ese instante:

$x=v\cdot (t-3)$

$\mathcal{E}=- \cfrac{d \left(B\cdot \bigl(v\cdot (t-3)\bigr)^2\right)}{dt}$

$\mathcal{E}=- \cfrac{d \left(B\cdot v^2\cdot (t^2-6t+9)\right)}{dt}$

Sustituimos los valores que sabemos en la ecuación:

$\mathcal{E}=- \cfrac{d \left(0,4\cdot 2^2\cdot (t^2-6t+9)\right)}{dt}$

$\mathcal{E}=- \cfrac{d \left(1,6 \cdot (t^2-6t+9)\right)}{dt}$

$\mathcal{E}=- \cfrac{d \left(1,6t^2-9,6t+14,4)\right)}{dt}$

Y luego calculamos la derivada para obtener la expresión de la tensión inducida en función del tiempo:

$\mathcal{E}=- (2\cdot 1,6t-9,6)$

$\mathcal{E}=- 3,2t+9,6$

Por lo tanto, el valor de la tensión inducida en el instante t=5 s es:

$\mathcal{E}=- 3,2 \cdot 5+9,6=-6,4 \ V$

Ejercicio 2

Una espira rectangular de dimensiones 3×4 cm penetra en una región de campo magnético uniforme $\vv{B}=-0,3\vv{k} \ T$ con una velocidad constante de $\vv{v}=5\vv{i} \ cm/s$ . Calcula la fuerza electromotriz inducida y la corriente inducida si la resistencia de la espira es de 12 Ω.

Ver solución

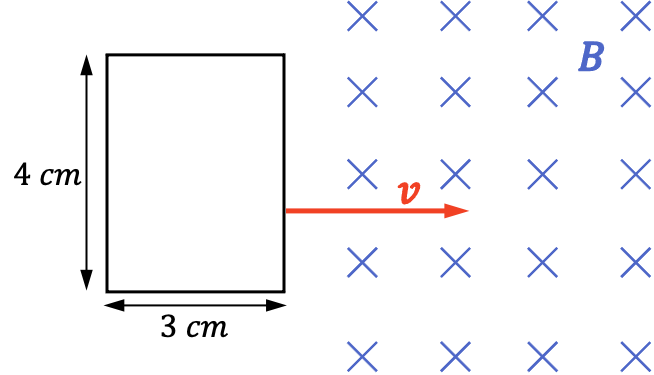
A medida que la espira avanza, la superficie en el interior del campo magnético es mayor, por lo que el flujo magnético también es mayor. Entonces, como hay una variación del flujo magnético, habrá una fuerza electromotriz inducida.

Para calcular la expresión que define la tensión inducida, tenemos que aplicar la fórmula de la ley de Faraday-Lenz:

$\mathcal{E}=- \cfrac{d \Phi }{dt}$

El flujo magnético es igual al producto del campo magnético por la superficie por el coseno del ángulo que forman el vector del campo con el vector normal, por tanto:

$\mathcal{E}=- \cfrac{d \bigl(B\cdot S\cdot \text{cos}(0^{\text{o}})\bigr)}{dt}$

$\mathcal{E}=- \cfrac{d \left(B\cdot S\right)}{dt}$

La superficie de la fórmula se refiere al área que está dentro de la región de campo magnético. Esta superficie depende de la posición de la espira, que se va moviendo. Así pues, si llamamos x a la longitud de espira que está dentro de la zona magnética, dicha superficie equivale a x por la altura de la espira, que es 4 cm:

$\mathcal{E}=- \cfrac{d \left(B\cdot x\cdot 0,04\right)}{dt}$

Ahora tenemos que sustituir la variable x por una expresión equivalente que dependa del tiempo. Como sabemos la velocidad a la que avanza la espira, podemos sustituir la variable x por el producto entre la velocidad y el tiempo

$x=v\cdot t$

$\mathcal{E}=- \cfrac{d \left(B\cdot v\cdot t \cdot 0,04\right)}{dt}$

Sustituimos los valores que conocemos en la ecuación:

$\mathcal{E}=- \cfrac{d \left(-0,3 \cdot 0,05\cdot t \cdot 0,04\right)}{dt}$

$\mathcal{E}=- \cfrac{d \left(-0,0006 \cdot t\right)}{dt}$

Resolvemos la derivada:

$\mathcal{E}=0,0006 \ V$

Una vez hemos calculado la fuerza electromotriz inducida, podemos determinar la intensidad de la corriente eléctrica inducida mediante la ley de Ohm:

$\begin{aligned}I&=\cfrac{\mathcal{E}}{R}\\[2ex]I&=\cfrac{0,0006}{12}\\[2ex]I&=5\cdot 10^{-5} \ A\end{aligned}$

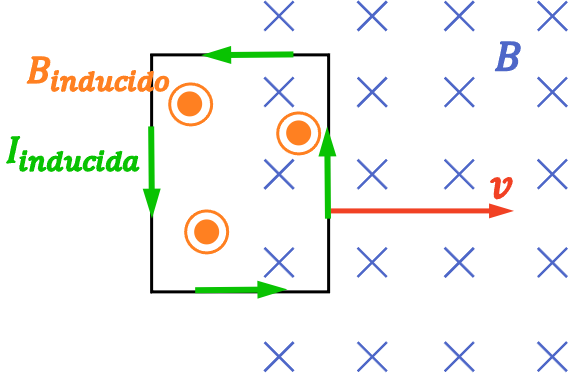
Según la ley de Lenz, el campo magnético inducido debe tener el sentido opuesto al campo magnético que lo ha provocado, por lo tanto, el campo magnético inducido será hacia fuera del plano de la pantalla. En consecuencia, por la regla de la mano derecha deducimos que el sentido de la corriente eléctrica es antihorario.

Aplicaciones de la inducción electromagnética

Aunque pueda parecerte un fenómeno muy extraño, la inducción electromagnética tiene muchas aplicaciones en la vida cotidiana, a continuación te mostramos las más importantes:

Generadores eléctricos: los generadores eléctricos funcionan mediante la inducción electromagnética, de modo que la gran mayoría de electricidad que usamos en el día a día es generada mediante la inducción electromagnética.
Transformadores: los transformadores son dispositivos que utilizan la inducción electromagnética para transferir energía eléctrica de un circuito a otro.
Cargas inalámbricas: la inducción electromagnética también se usa en tecnologías de carga inalámbrica, por ejemplo en la carga inalámbrica de teléfonos móviles. La energía se transfiere de una bobina de transmisión a una bobina de recepción mediante campos electromagnéticos.
Electroimanes: los electroimanes son dispositivos temporales que producen un campo magnético cuando una corriente eléctrica pasa a través de ellos. Se utilizan en una variedad de aplicaciones, como en motores eléctricos, dispositivos de levitación magnética y en la industria para levantar objetos metálicos pesados.

¿Qué es la inducción electromagnética?

Fórmula de la inducción electromagnética

Ejercicios resueltos de la inducción electromagnética

Ejercicio 1

Ejercicio 2

Aplicaciones de la inducción electromagnética

Deja un comentario Cancelar respuesta