▷ Ley de Lenz

En este post te explicamos en qué consiste la ley de Lenz y para qué sirve. Así pues, encontrarás qué dice la ley de Lenz, cuál es su fórmula y, además, un ejemplo resuelto de su aplicación.

Índice

¿Qué es la ley de Lenz?

La ley de Lenz es una ley del electromagnetismo que establece que la dirección de la corriente inducida debida a la variación del flujo magnético es contraria al movimiento que la provoca.

Cuando varía el flujo magnético que atraviesa una superficie, se produce una inducción electromagnética, es decir, se induce una corriente eléctrica sin necesidad de establecer contacto físico. Así pues, la ley de Lenz dice que la corriente eléctrica inducida se opone al movimiento que la produjo.

La ley de Lenz se llama así en honor al físico Heinrich Lenz, quien descubrió dicha fórmula en 1834.

Fórmula de la ley de Lenz

La ley de Lenz está relacionada con la ley de Faraday, la cual establece que cuando varía el flujo magnético se induce una tensión (fuerza electromotriz) proporcional a la variación temporal del flujo magnético.

A esta regla, la ley de Lenz añade que el sentido de la tensión inducida es tal que su efecto se opone a la causa que lo generó.

Por lo tanto, en términos prácticos, la ley de Lenz añade un signo negativo a la fórmula de la ley de Faraday. Este signo indica que la tensión inducida es contraria al movimiento que la provoca.

$\mathcal{E}=\color{red}\bm{-}\color{black}\cfrac{d \Phi }{dt}$

En el caso de una bobina, la fuerza electromotriz inducida también es proporcional al número de espiras de esta:

$\mathcal{E}=\color{red}\bm{-}\color{black}N\cdpt \cfrac{d \Phi }{dt}$

Donde:

$\mathcal{E}$ es la tensión inducida o fuerza electromotriz (fem), expresada en voltios (V).
$\Phi$ es el flujo magnético, expresado en webers (Wb).
$\cfrac{d \Phi }{dt}$ es la tasa de variación temporal del flujo magnético.
$N$ es el número de espiras de la bobina.

Como la ley de Lenz y la ley de Faraday están relacionadas, de hecho, comparten la misma fórmula, muchas veces esta regla se llama ley de Faraday-Lenz.

Ejercicio resuelto de la ley de Lenz

Una espira rectangular de dimensiones 3×4 cm penetra en una región de campo magnético uniforme $\vv{B}=-0,3\vv{k} \ T$ con una velocidad constante de $\vv{v}=5\vv{i} \ cm/s$ . Calcula la fuerza electromotriz inducida y la corriente inducida si la resistencia de la espira es de 12 Ω.

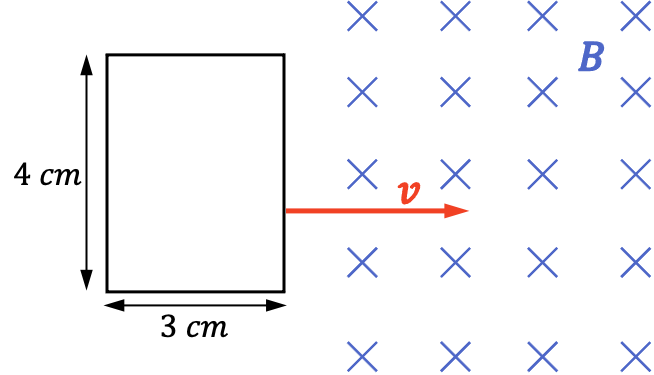
A medida que la espira avanza, la superficie en el interior del campo magnético es mayor, por lo que el flujo magnético también es mayor. Entonces, como hay una variación del flujo magnético, habrá una fuerza electromotriz inducida.

Para calcular la expresión que define la tensión inducida, tenemos que aplicar la fórmula de la ley de Faraday-Lenz:

$\mathcal{E}=- \cfrac{d \Phi }{dt}$

El flujo magnético es igual al producto del campo magnético por la superficie por el coseno del ángulo que forman el vector del campo con el vector normal, por tanto:

$\mathcal{E}=- \cfrac{d \bigl(B\cdot S\cdot \text{cos}(0^{\text{o}})\bigr)}{dt}$

$\mathcal{E}=- \cfrac{d \left(B\cdot S\right)}{dt}$

La superficie de la fórmula se refiere al área que está dentro de la región de campo magnético. Esta superficie depende de la posición de la espira, que se va moviendo. Así pues, si llamamos x a la longitud de espira que está dentro de la zona magnética, dicha superficie equivale a x por la altura de la espira, que es 4 cm:

$\mathcal{E}=- \cfrac{d \left(B\cdot x\cdot 0,04\right)}{dt}$

Ahora tenemos que sustituir la variable x por una expresión equivalente que dependa del tiempo. Como sabemos la velocidad a la que avanza la espira, podemos sustituir la variable x por el producto entre la velocidad y el tiempo

$x=v\cdot t$

$\mathcal{E}=- \cfrac{d \left(B\cdot v\cdot t \cdot 0,04\right)}{dt}$

Sustituimos los valores que conocemos en la ecuación:

$\mathcal{E}=- \cfrac{d \left(-0,3 \cdot 0,05\cdot t \cdot 0,04\right)}{dt}$

$\mathcal{E}=- \cfrac{d \left(-0,0006 \cdot t\right)}{dt}$

Resolvemos la derivada:

$\mathcal{E}=0,0006 \ V$

Una vez hemos calculado la fuerza electromotriz inducida, podemos determinar la intensidad de la corriente eléctrica inducida mediante la ley de Ohm:

$\begin{aligned}I&=\cfrac{\mathcal{E}}{R}\\[2ex]I&=\cfrac{0,0006}{12}\\[2ex]I&=5\cdot 10^{-5} \ A\end{aligned}$

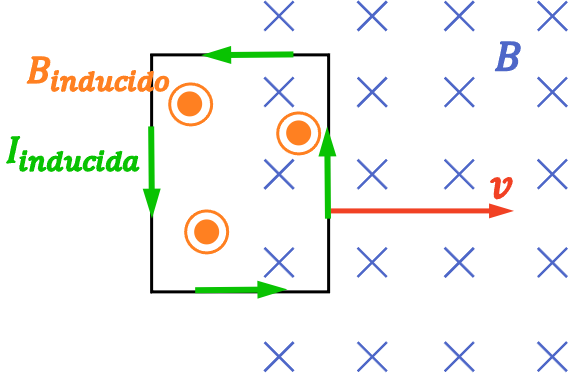
Según la ley de Lenz, el campo magnético inducido debe tener el sentido opuesto al campo magnético que lo ha provocado, por lo tanto, el campo magnético inducido será hacia fuera del plano de la pantalla. En consecuencia, por la regla de la mano derecha deducimos que el sentido de la corriente eléctrica es antihorario.

➤ Ver: Ejercicio resuelto de la ley de Lorentz

Aplicaciones de la ley de Lenz

La ley de Lenz tiene varias aplicaciones en ingeniería, a continuación te mostramos las más habituales:

Frenado electromagnético: la ley de Lenz se utiliza en aplicaciones de frenado de trenes y en sistemas de seguridad en ascensores. Cuando un tren o un ascensor necesitan frenar, el movimiento relativo entre un imán y una bobina genera una corriente inducida que crea un campo magnético opuesto al campo magnético original, lo que produce una fuerza de frenado.
Transformadores: los transformadores funcionan gracias a la ley de Lenz. Cuando se aplica un voltaje alterno a una bobina primaria, se crea un campo magnético cambiante en el núcleo del transformador. Esto induce un voltaje en la bobina secundaria, que puede ser de mayor o menor voltaje dependiendo del número de vueltas en cada bobina.
Amortiguadores magnéticos: la ley de Lenz también se aplica en sistemas de suspensión de vehículos y en equipos de precisión para reducir vibraciones. Un sistema de amortiguación magnética utiliza corrientes inducidas para generar campos magnéticos que se oponen al movimiento relativo entre dos objetos, reduciendo así la vibración.

¿Qué es la ley de Lenz?

Fórmula de la ley de Lenz

Ejercicio resuelto de la ley de Lenz

Aplicaciones de la ley de Lenz

Deja un comentario Cancelar respuesta