En este post se explica qué es la fuerza electromotriz inducida. También encontrarás cómo calcular la fuerza electromotriz inducida y, además, un ejemplo resuelto paso a paso.
Índice
¿Qué es la fuerza electromotriz inducida?
La fuerza electromotriz inducida, abreviada como f.e.m. o fem, es el voltaje que induce un campo magnético a un circuito cerrado.
La fuerza electromotriz inducida también se conoce como voltaje inducido o electromotancia.
Gracias al fenómeno de la inducción electromagnética, un campo magnético puede inducir electricidad a un circuito cerrado cuando se produce una variación del flujo magnético. Así pues, el potencial que induce el campo magnético y permite generar esta corriente eléctrica inducida se llama fuerza electromotriz inducida.
La fuerza electromotriz se expresa en voltios (V), ya que es un potencial eléctrico.
A pesar de su nombre, la fuerza electromotriz inducida no es un tipo de fuerza, sino que se trata de un tipo de voltaje. Por tanto, la fuerza electromotriz inducida se puede relacionar con la intensidad de la corriente y la resistencia de un circuito mediante la ley de Ohm, más abajo veremos cómo se hace.
Fórmula de la fuerza electromotriz inducida
La fuerza electromotriz inducida se produce cuando ocurre una variación del flujo magnético en el tiempo. Es decir, cuando el flujo de campo magnético que atraviesa una superficie cambia de valor, se induce una fuerza electromotriz en el circuito.
En concreto, la fuerza electromotriz inducida es igual a la variación temporal del flujo magnético cambiado de signo. Por lo tanto, la fórmula de la fuerza electromotriz inducida es ε=-dΦ/dt.
Si tenemos como inductor una bobina con N espiras, tenemos que multiplicar la fórmula anterior por el número de espiras:
Donde:
es la fuerza electromotriz inducida (fem), expresada en voltios (V).
es el flujo magnético, expresado en webers (Wb).
es la tasa de variación temporal del flujo magnético.
es el número de espiras de la bobina.
Ten en cuenta que el flujo magnético puede variar por diferentes motivos: por un cambio en la intensidad del campo magnético, por un movimiento de la fuente del campo magnético, por un giro de la superficie que atraviesa el flujo magnético, etc.
Esta fórmula se conoce como ley de Faraday, ya que la descubrió Michael Faraday con un experimento en 1831.
Ejercicio resuelto de la fuerza electromotriz inducida
- Una espira rectangular de dimensiones 3×4 cm penetra en una región de campo magnético uniforme
con una velocidad constante de 
. Calcula la fuerza electromotriz inducida y la corriente inducida si la resistencia de la espira es de 12 Ω.
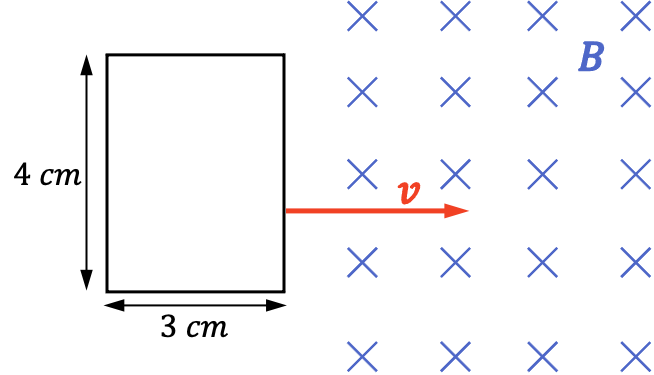
A medida que la espira avanza, la superficie en el interior del campo magnético es mayor, por lo que el flujo magnético también es mayor. Entonces, como hay una variación del flujo magnético, habrá una fuerza electromotriz inducida.
Para calcular la expresión que define la tensión inducida, tenemos que aplicar la fórmula de la ley de Faraday:
El flujo magnético es igual al producto del campo magnético por la superficie por el coseno del ángulo que forman el vector del campo con el vector normal, por tanto:
La superficie de la fórmula se refiere al área que está dentro de la región de campo magnético. Esta superficie depende de la posición de la espira, que se va moviendo. Así pues, si llamamos x a la longitud de espira que está dentro de la zona magnética, dicha superficie equivale a x por la altura de la espira, que es 4 cm:
Ahora tenemos que sustituir la variable x por una expresión equivalente que dependa del tiempo. Como sabemos la velocidad a la que avanza la espira, podemos sustituir la variable x por el producto entre la velocidad y el tiempo
Sustituimos los valores que conocemos en la ecuación:
Resolvemos la derivada:
Una vez hemos calculado la fuerza electromotriz inducida, podemos determinar la intensidad de la corriente eléctrica inducida mediante la ley de Ohm:
![\begin{aligned}I&=\cfrac{\mathcal{E}}{R}\\[2ex]I&=\cfrac{0,0006}{12}\\[2ex]I&=5\cdot 10^{-5} \ A\end{aligned}](https://www.ingenierizando.com/wp-content/ql-cache/quicklatex.com-80b2df3d330839762edc70ce546bd7b2_l3.svg "Rendered by QuickLaTeX.com")
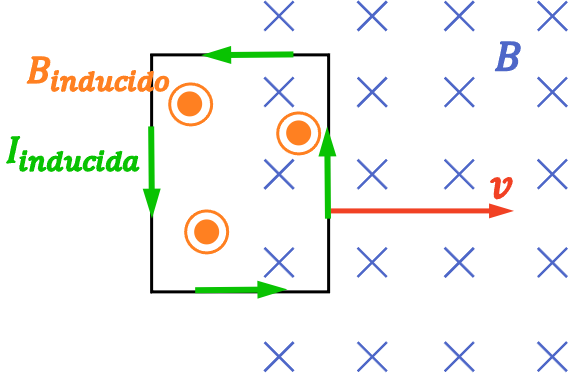
Según la ley de Lenz, el campo magnético inducido debe tener el sentido opuesto al campo magnético que lo ha provocado, por lo tanto, el campo magnético inducido será hacia fuera del plano de la pantalla. En consecuencia, por la regla de la mano derecha deducimos que el sentido de la corriente eléctrica es antihorario.
